Qwen2.5-32B大模型Self-Attention算子推理流程详解

本文将以 Qwen2.5-32B 大语言模型为例，详细拆解其在推理过程中，Self-Attention 模块的核心算子计算逻辑。我们将以尽量简洁的形式讲述核心流程，部分细节（如 Linear 层的偏置项）会被暂时忽略。

Attention 的推理流程概览

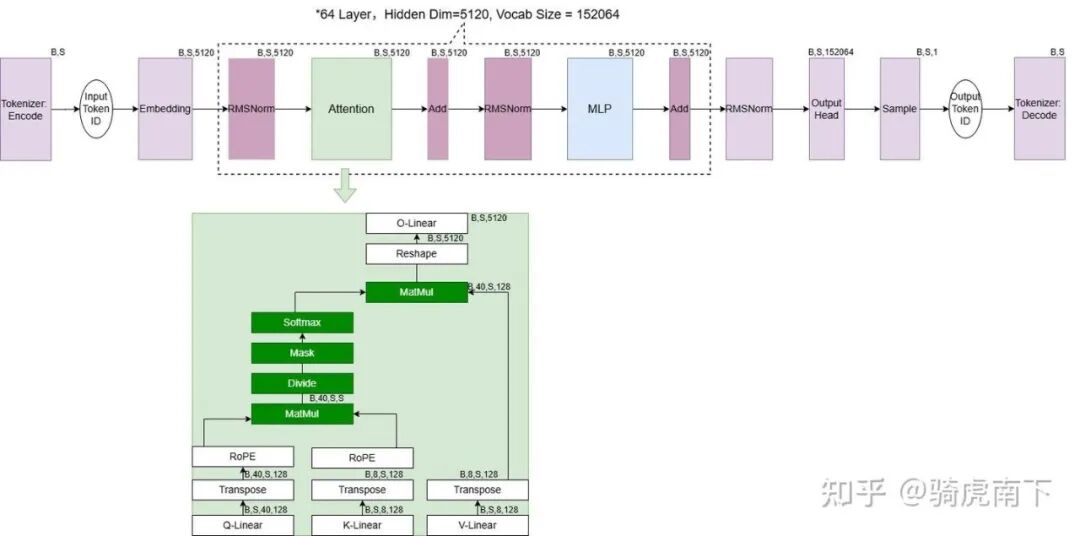
如上图所示，模型的流程从左到右，而 Attention 算子内部的数据流自下而上。当激活（Activation）数据流入 Attention 模块后，主要经历以下几个步骤：

1. QKV投影：同一份输入数据分别经过 Q-Linear、K-Linear、V-Linear 三个线性层，得到查询（Q）、键（K）、值（V）三个矩阵。
2. 位置编码：将 Q 与转置后的 K 分别进行 RoPE（旋转位置编码）处理。
3. 注意力计算：将编码后的 Q、K 与转置后的 V 送入 GQA（分组查询注意力）模块进行核心计算。
4. 输出投影：将 GQA 的输出进行 Reshape 后，再通过一次 O-Linear 线性层，得到整个 Attention 模块的最终输出。

其中，B（Batch）表示输入的请求批次大小，S（Sequence Length）表示输入序列的长度。例如 Shape [B, S, 5120] 表示当前算子输出的激活数据维度，5120 是模型的隐藏层大小。

QKV-Linear 算子：生成查询、键、值

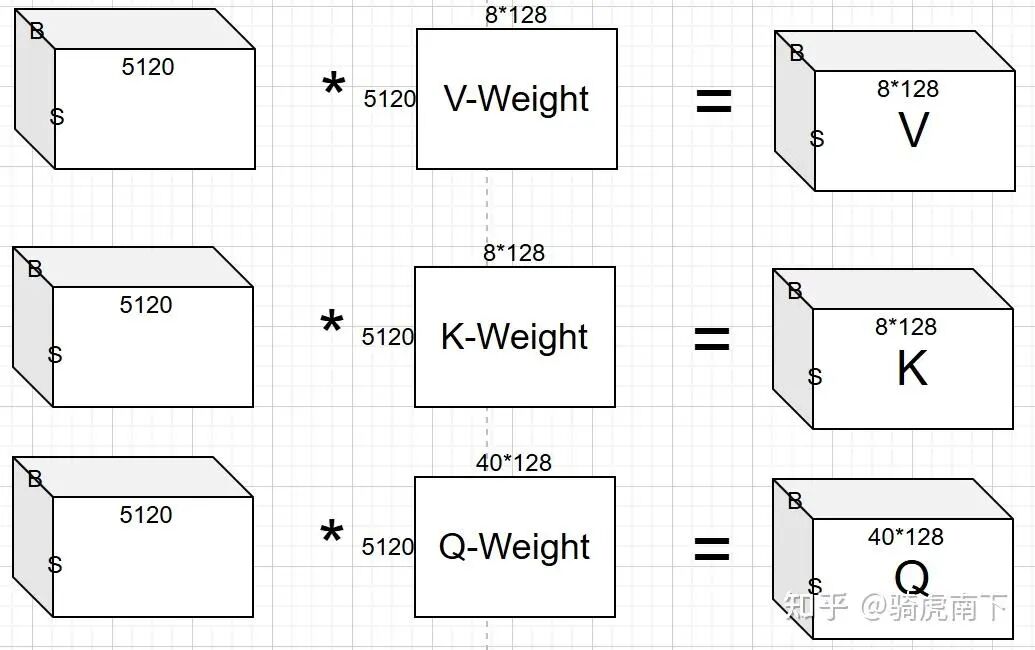
经过 Embedding 或 RMSNorm 层后，输入 Attention 模块的激活数据是一个三维矩阵，Shape 为 [B, S, 5120]。

以生成查询（Q）矩阵为例：Q 权重矩阵的宽度为 5120（即 40个注意力头 * 每个头维度128）。计算时，每个批次（Batch）中每个词元（Token）对应的 5120 个隐藏状态值（矩阵中的一行），与权重矩阵中的 5120 个值（一列）进行乘累加运算，最终得到 Q 矩阵在对应位置的一个输出值。K 和 V 的生成过程与此类似。

RoPE 算子：融入位置信息

以查询（Q）矩阵作为 RoPE 的输入为例，在转置（Transpose）后其 Shape 变为 [B*40, S, 128]。RoPE 会对每个注意力头（Head）的数据独立进行操作。

如下图所示，我们取某个批次、某个注意力头、某个词元对应的 128 维向量 {x_0, x_1, ..., x_127}。将前 64 个数据与后 64 个数据两两配对，分别应用以下公式进行计算，从而得到经过 RoPE 位置编码后的输出 Q-RoPE。

（注：为聚焦核心算子逻辑，此处省略了旋转角 θ 的具体计算以及 RoPE 的算法原理详解。）

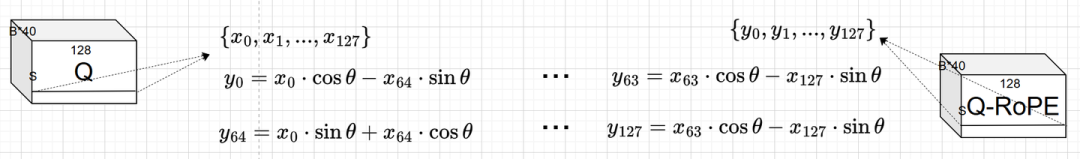
GQA 算子：核心注意力计算

GQA（分组查询注意力）的计算过程可以分解为四个主要步骤，这也是大语言模型推理中的核心计算环节，其背后的算法设计直接影响了模型的性能和效率。

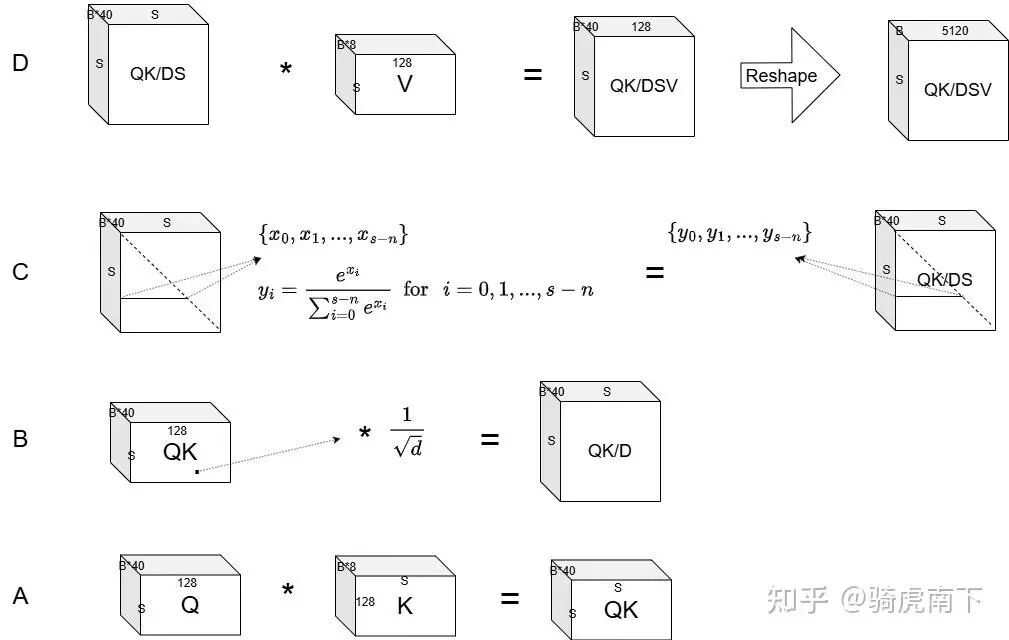
A. 计算注意力分数矩阵
如下图A所示，将 Q 与 K 在对应的批次、注意力头和词元维度上，对它们的 128 维向量进行点积（乘累加），得到原始的注意力分数矩阵 QK。

B. 缩放
如下图B所示，为防止点积结果过大导致后续 Softmax 函数的梯度消失，将 QK 矩阵中的每个值除以一个缩放因子 √dk（dk 为注意力头维度，此处为128），得到缩放后的矩阵 QK/D。

C. Mask 与 Softmax
如下图C所示，首先对 QK/D 矩阵应用一个倒三角 Mask（因果掩码），其作用是确保当前词元只能关注到它自身及之前的词元。然后对掩码后的矩阵进行 Softmax 归一化，将分数转化为概率分布，得到矩阵 QK/DS。

D. 加权求和
如下图D所示，将 Softmax 输出后的概率矩阵 QK/DS，与值（V）矩阵在对应维度上进行加权求和（乘累加），得到最终的注意力输出矩阵 QK/DSV。

需要注意的是，在 GQA 机制中，并非传统的多头注意力（MHA）。此处，Q 的每 5 个注意力头会共享同一个 K 头和 V 头。

Output-Linear 算子：输出投影

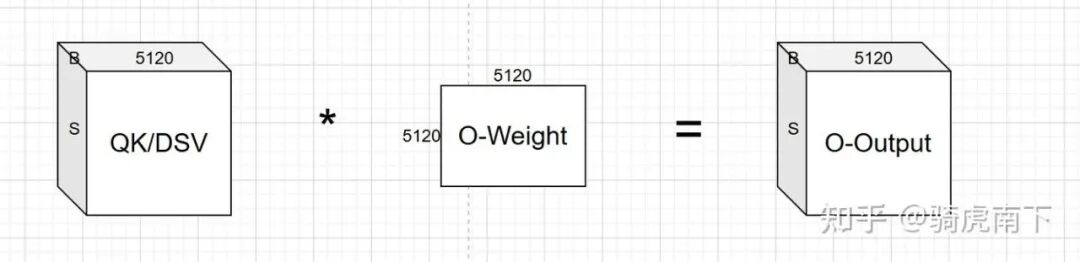
最后一步，将 GQA 模块的输出矩阵 QK/DSV 进行 Reshape 后，与输出投影层（O-Linear）的权重矩阵进行矩阵乘法运算，得到整个 Attention 模块的最终输出 O-Output。

至此，我们完成了从输入激活到输出激活的完整 Self-Attention 算子前向推理流程的解析。理解这些基础算子的计算逻辑，是深入优化大模型推理性能和进行相关人工智能应用开发的重要基石。