TL;DR
DeepSeek 发布了一篇题为《mHC: Manifold-Constrained Hyper-Connections》[1]的新论文。这篇论文的品味非常好,一方面在算法层面,巧妙运用了流形 (Manifold) 概念和基于最优传输 (Optimal Transport) 理论的 Sinkhorn-Knopp 算法;另一方面,其工程实现上的处理也非常优雅。
事实上,在 2024 年字节发布 Hyper-Connections 的几个月前,我曾撰写过一篇文章《谈谈DeepMind会做算法导论的TransNAR并引出基于SAE-GNN的可组合Transformer猜想》,探讨过一个基于可解释性视角的架构,其核心思想类似于通过 SAE 和 TransNAR 的方式来扩展残差流的宽度和连接的多样性。
更进一步,从范畴论的视角看,如果将 Attention 视作一种态射,那么就需要一些高阶范畴来施加约束,这其实才是 Hyper-Connection 的实质,而不仅仅是当下一些算法工程师简单理解的残差处理。在展开分析 mHC 之前,我们先补充一些相关的数学背景。本文目录如下:
0. 一些数学的背景
0.1 Manifold视角
0.2 Hyper-Connection Overview
0.3 基于范畴论的视角看Hyper-Connection
0.4 Optimal Transport
1. mHC Overview
1.1 HC如何破坏恒等映射
1.2 Mainfold Constrained
2. 相关工作
2.1 微观设计
2.2 宏观设计
3. 预备知识
3.1 数值稳定性分析
3.2 系统开销
4. mHC算法和实现
4.1 流形约束超连接
4.2 参数化与流形投影
4.3 mHC工程实现
4.3.1 算子融合
4.3.2 Recomputing
4.3.3 流水线排布
5. 实验
5.1 Setup
5.2 主要结果
5.3 Scaling
5.4 稳定性分析
6. 结论和展望
0. 一些数学的背景
mHC 本身的实现非常简洁明了,但为了更透彻地理解其背后的思想,并展望其未来可能的扩展,这里有必要先展开阐述一下流形和 Hyper-Connection 的概念。毕竟,流形约束的应用潜力可能不仅限于提升 HC 的训练稳定性,或许还能扩展到其他方面,比如基于流形约束来控制 Attention?DeepSeek 在论文结尾也提到:该框架同样支持探索为特定学习目标量身定制的、多样化的流形约束。
因此,在这一前置章节中,我想更多地展开这些数学观念,虽然其中一些内容与 mHC 本身并无最直接的关联。
0.1 Manifold视角
我们先用一个比较浅显的例子来解释一下流形 (Manifold)。这个观点源于 DeepMind 的 Demis Hassabis,他眼中的大千世界存在着某种结构压缩的低维流形。
Hassabis 在解释 AlphaFold 成功的关键时指出,蛋白质的理论构象空间是天文数字级别的,完全无法穷举或进行物理模拟。但自然界中的蛋白质能在毫秒级自动完成折叠,这说明自然并没有在“全空间乱跑”,而是被压缩并演化在一条低维流形上。这正是 AlphaFold 能够成功预测结构的根本前提。他强调:自然现象之所以“可预测”,不是因为我们写出了完美的方程,而是因为自然的行为模式在高维空间中稀疏分布、结构清晰、路径稳定,它们集中在一种可压缩、可调度的结构空间中,这就是所谓的“流形”。
AlphaFold 并非像传统方法那样模拟蛋白质在全空间内的动力学演化过程,而是通过从海量蛋白质序列与已知结构的样本中学习,捕捉到了这个结构流形。它不是试图穷举所有可能构象,而是在训练中逐步内化出一个可以导航的、从序列到结构的映射空间,即一个“潜在折叠流形”。最终,在预测新蛋白结构时,它并非搜索整个空间,而是在这个内化的流形中直接定位最可能的位置,从而高效完成预测。
另一个例子是具身智能,一个机器人的所有可能状态 (如关节角度、位置、姿态) 可以构成一个流形。例如,三维空间中刚体的姿态 (旋转) 可以由一个三维流形 SO(3) 来描述。

从更宏观的时间尺度来看,历史长河中的世界万物如同一个流形 (Manifold) 静静流淌,而文字形成的记忆和智能则将时空折叠成一个高维空间... 似乎大语言模型 (LLM) 的训练也遵循类似的原理。
换言之,世界本是高熵混沌的,但其中蕴含可提取的结构秩序。只要识别出这些结构,就能实现压缩、调度与迁移,从而在无序中建立智能与控制。以前,我们把这些结构秩序用自然语言称为“经验”或总结成“定理”。而现在,深度神经网络 正从数据中提取出低维流形,并在这个结构压缩的空间中完成调度和推理。它的智能不在于重建现实,而在于压缩现实,将其压缩成一个可以学习、调用、迁移的结构流形。
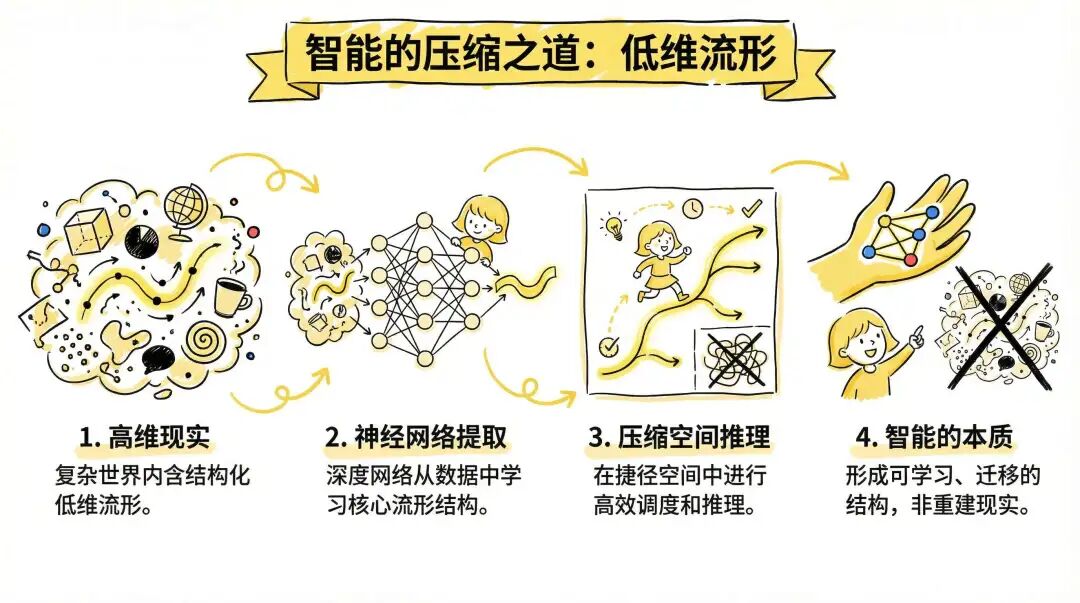
结论:利用流形对深度神经网络施加一些可学习的约束,成了一条非常直接的路径。那么,问题来了:这些约束应该施加在神经网络的什么地方?mHC 就是一个绝佳的例子。
0.2 Hyper-Connection Overview
我们先来简要阐述一下《Hyper-Connection》[2],这是字节在 2024 年 9 月的一项工作,Defa 在知乎上有一篇通俗的解释《都2025年了,我不允许你还在用残差连接!》[3]。
Transformer 中的残差连接主要有 Pre-Norm 和 Post-Norm 两种变体,各自都有其局限性(苏剑林的博客有过详细分析)。
- Pre-Norm:在每个残差块之前做 Norm,能有效减少梯度消失问题。但其问题在于,后面的层输出过于相似,削弱了模型的学习能力。
- Post-Norm:在残差块之后做 Norm,有助于减少表示崩溃问题,但会重新引入梯度消失问题。
Hyper-Connections 的核心在于,通过动态调整不同层之间的连接权重,弥补了残差连接在梯度消失和表示崩溃之间的“跷跷板”现象。最终发现,它不仅训练比 Pre-Norm 更稳定,层间相似度更低、范围更广,效果也更好。
问题的根源在于,传统的残差连接以一种固定的、不可学习的方式来组合层输入和输出。能否让网络自主学习如何组合不同层级的特征,以打破这种固定权衡?为了实现这一点,HC 引入了两个关键概念:宽度扩展和可学习的连接。Hyper-Connection 在 Transformer 上的完整网络结构如下:
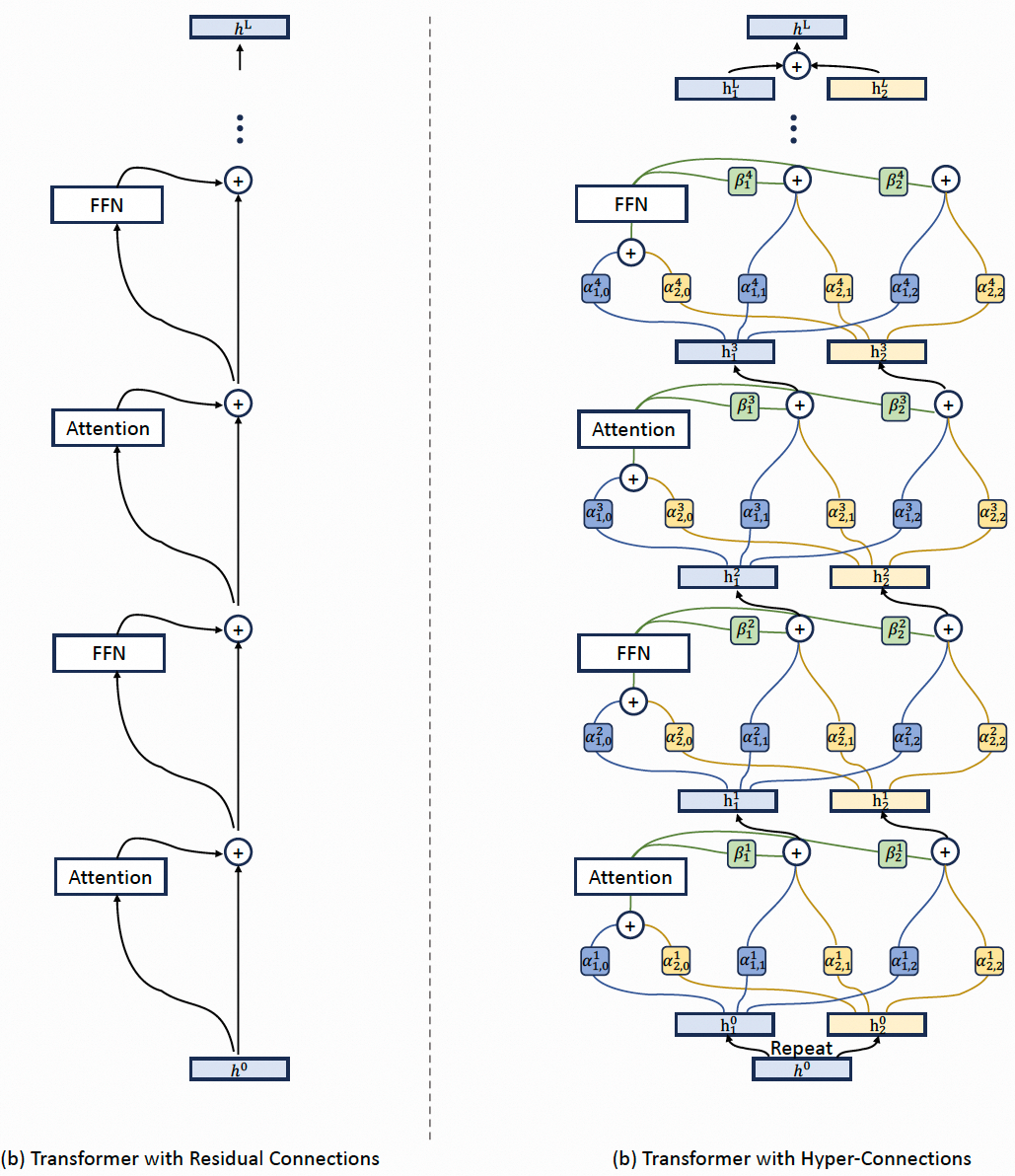
后续的工作是字节的《Virtual Width Networks》[4]。
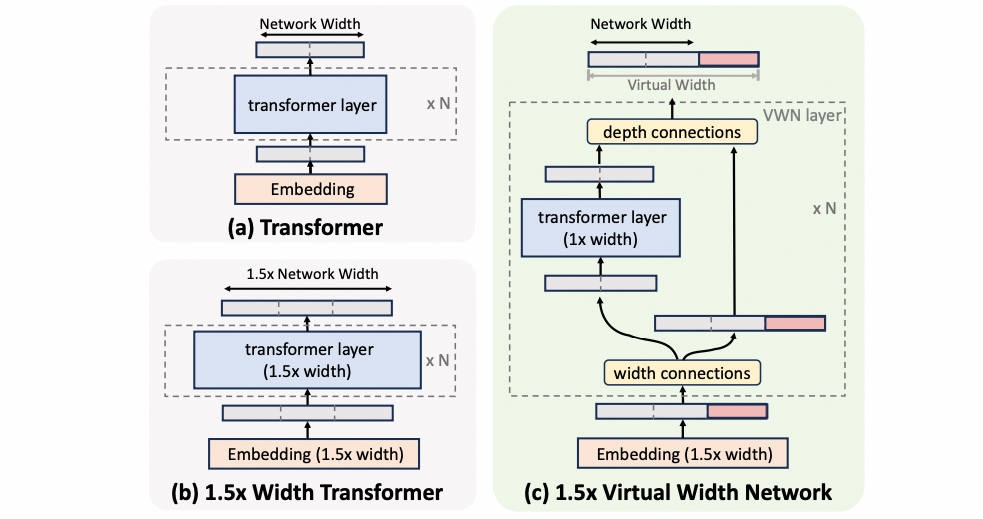
Hyper-Connections 对 hidden 向量建立以下两类连接:
- 深度连接:类似于残差连接,但通过为输入与输出之间的连接分配可学习的权重,允许网络灵活调整不同层之间的连接强度。
- 宽度连接:在每一层中实现 Hidden 向量之间的信息交互,增强特征融合能力,从而提升模型的表示效果。
我们以 Dynamic HC (DHC) 为例,来简单解释一下算法。
将第 k 层的输入视为隐向量 $h^{k-1}$ (或 $x^{k-1}$),网络的初始输入为 $x^0$。最初,$x^0$ 被复制 n 次,形成初始的超隐状态矩阵 $H^0 = [x^0, x^0, ..., x^0]^T \in \mathbb{R}^{n \times d}$。
对于第 k 层,其输入是来自前一层的超隐状态矩阵 $H^{k-1}$。
Hyper-Connection 可以用一个矩阵 $HC^k$ 来表示,其中每个元素定义了一个连接权重。
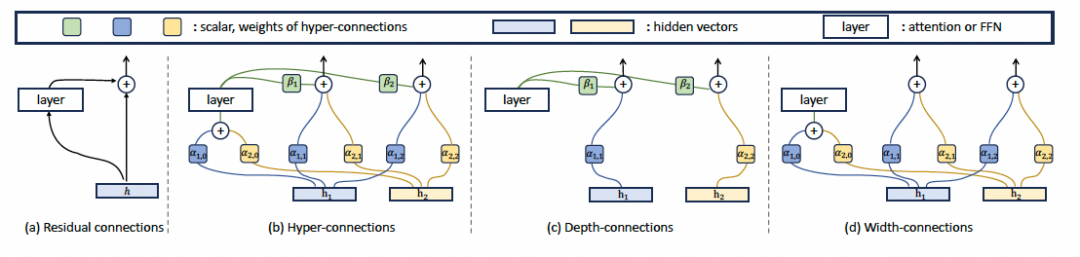
深度连接关注垂直方向的信息流动,即输入与输出之间的关系,如上图 (c) 所示。深度连接可以被解耦为矩阵 $H_{depth}$。
宽度连接关注水平方向的信息流动,即通道与通道之间的关系,如上图 (d) 所示,矩阵 $H_{width}$ 可以类似定义。
简单来说:动态深度连接为每个 token 动态调整新旧知识在每个通道中的混合比例;动态宽度连接为每个 token 动态调整通道间的信息交换和汇聚方式,从而实现计算图上 Hidden Vector 的动态重排。
为了更便于理解,可以用一个“智能音频混合器”来类比 Dynamic Hyper-Connection:
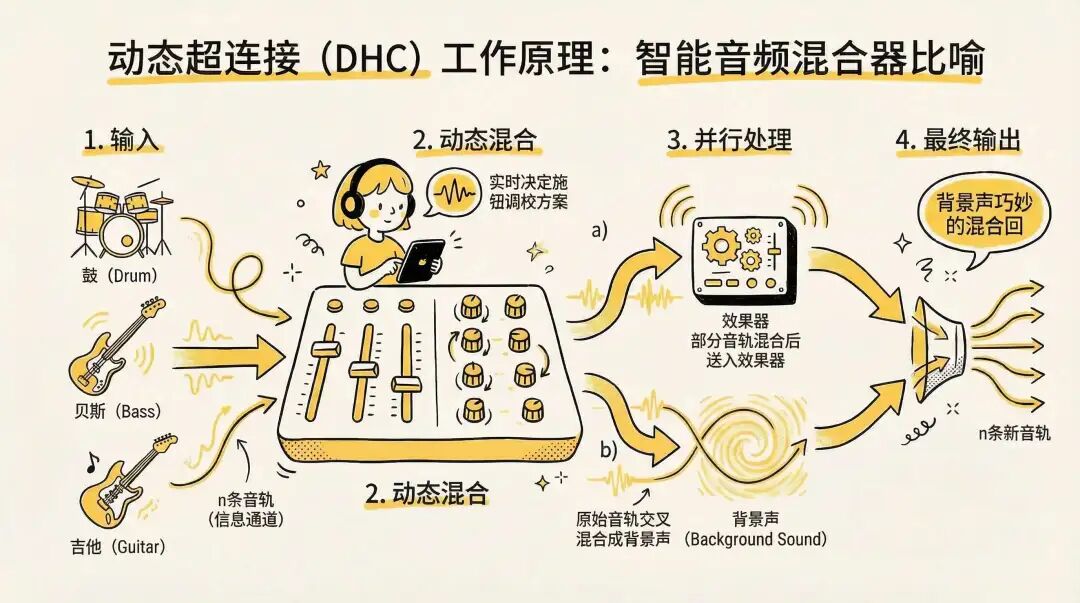
- 输入 H:想象有
n 条音轨 (例如,鼓,贝斯,吉他,人声),每条音轨都是一个信息通道。
- 步骤 1 (动态权重生成):混音师 (网络) 听了一下当前的音乐片段 (输入 token),决定了所有旋钮的调校方案 ($\theta^k$)。
- 步骤 2 (宽度连接):
h0 的计算:混音师根据 $\theta_{width}^k$ 方案,从 n 条音轨中混合出一个新的声音,送入一个效果器 (如混响,对应 T 层)。H‘ 的计算:同时,混音师根据 $\theta_{depth}^k$ 方案,对原始的 n 条音轨进行内部交叉混合,准备好作为背景声。
- 步骤 3 (核心计算):效果器处理混合声,产生新的效果声 $\tilde{h}^k$。
- 步骤 4 (深度连接):混音师根据 $\theta_{post}^k$ 方案,将效果声 $\tilde{h}^k$ 混合回
n 条背景声 $H'$ 中,形成最终输出的 n 条新音轨 $H^k$,传递给下一个混音站。
结合流形视角:我们可以将 DHC 理解为一种 自适应的、数据驱动的动态流形约束。
传统的残差连接 $x_{l+1} = x_l + F(x_l)$ 可以被看作一种最简单的流形约束。它假设 $F(x_l)$ 是一个在 $x_l$ 点的微小扰动或更新。因此,输出 $x_{l+1}$ 仍然非常靠近输入 $x_l$。如果 $x_l$ 在流形上,那么 $x_{l+1}$ 也大概率在流形附近。这就像在地球表面上走一小步,你仍然在地球表面上。实质上,这也阐述了残差连接的恒等映射。但这个约束是静态且统一的。无论数据点 $x_l$ 位于流形的哪个位置,它都采用完全相同的约束方式 (简单相加),它对流形本身的局部几何结构一无所知。
DHC 通过其多通道设计和动态权重,实现了一种 流形感知 的动态约束。DHC 的 n 个通道可以被理解为在学习一个动态的、局部的坐标系,这个坐标系近似了表示流形在当前点 H 处的切空间。超隐状态矩阵 $H^{k-1}$ 中的 n 个向量,可以被看作是张成一个 n 维子空间的基向量。
一旦有了这个局部坐标系 (切空间),DHC 的所有动态操作都可以被理解为在这个坐标系内进行的、有意义的几何变换。
- $\theta_{pre}$ 构成了一个在流形上的方向选择器,$h_0 = \theta_{pre} H$ 这个操作,是在由 n 个基向量张成的切空间中,进行动态的线性组合,形成一个特定的方向向量。
- $\theta_{depth}$ 构成了在流形上的局部线性变换器 (旋转/缩放),$H' = \theta_{depth} H$ 这个操作,是对 n 个基向量本身进行一次动态的线性变换。
- $\theta_{post}$ 构成了一个更新投影器,$H^k = H' + \theta_{post} \tilde{h}^k$ 这个操作,是将 T 层计算出的更新量 $\tilde{h}^k$,通过 $\theta_{post}$ 投影回 n 个新的基向量方向上。
由于 DHC 在每一步 (每一层) 都会重新评估当前位置的局部几何 (通过动态生成 $\theta$),它的逐层演进过程更有可能 沿着流形的内在曲率前进,从而更紧密地逼近表示空间中的 测地线流。这意味着从输入到输出,信息的演化路径更“自然”、更“高效”,避免了在弯路上走直线的浪费 (传统的 ResNet 像是在高维环境空间中走直线小步),从而获得更好的性能。
关于 HC 的训练稳定性问题,以及 mHC 的算法,我们将在稍后的章节展开。
0.3 基于范畴论的视角看Hyper-Connection
另一个视角来自范畴论。在《大模型时代的数学基础(2)》中有些简单介绍,米田引理 (Yoneda Lemma) 是范畴论的基石。其核心思想是:一个对象完全由它与范畴中所有其他对象的关系 (即“箭头”或“态射”) 所决定。换句话说,你不需要知道一个对象的“内部构造”,只需要知道它如何与外界“交互”,就能完全理解它。
对应来看,以范畴论的视角,一个 Token 可以被看作由它的 Attention 关系所决定。于是 Token 和 Attention 某种意义上可以构成一个范畴。当前的大模型训练实际上是在利用 Transformer 机制,通过 Attention 构造的态射来构建世界的一个可表示的预层。
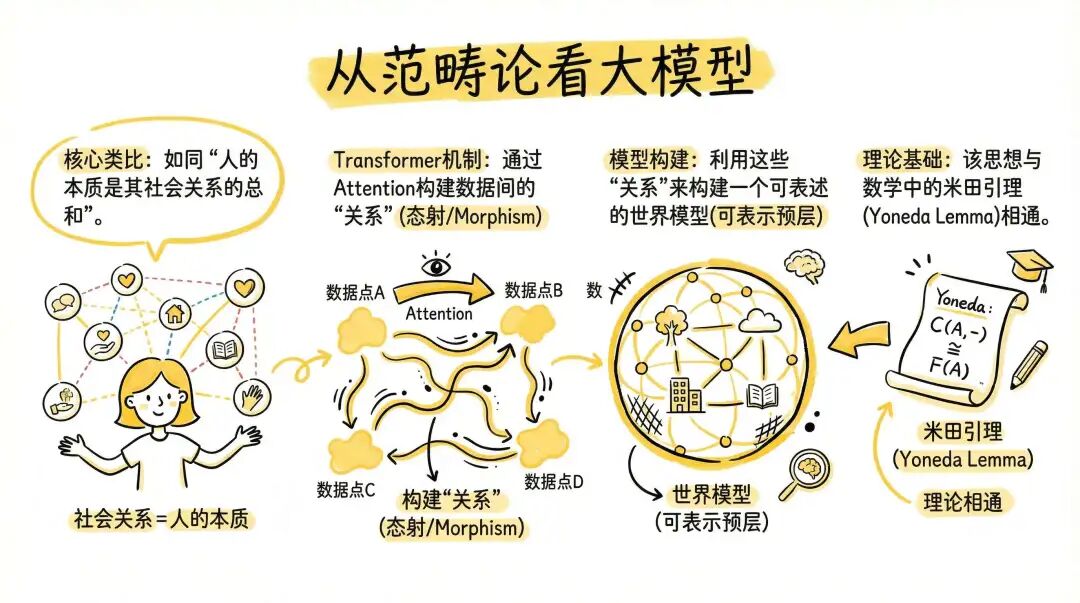
那么在这个视角下,结合流形的观点,我们就需要对模型本身的 Attention 施加一些约束。很自然的想法就是在 Attention 旁路上添加运算,进而引出 Hyper-Connection。更进一步,这些信息在模型层间的传递,又引出了范畴论中的 Nerve[5] 构造。具体内容可以参考《谈谈 Hierarchical Sparse Attention (HSA)》的第三章。
DeepSeek 进一步将流形约束的想法与 Hyper-Connection 结合,完成了提升 Hyper-Connection 训练稳定性的工作。
0.4 Optimal Transport
另一个需要补充的背景是 DeepSeek 所使用的 Sinkhorn-Knopp 算法,它源于最优传输理论。从最优传输的视角看 Attention 也是一个非常有趣的话题。
Sinkhorn Attention 是一个双向匹配:算法的目的是在 Query 和 Key 之间找到一个“最优匹配”或“最优运输方案”,使得分配满足双随机条件(行、列和均为 1)。排序矩阵通过 Sinkhorn-Knopp 迭代被强制变为双随机矩阵,保证了可导且可并行。
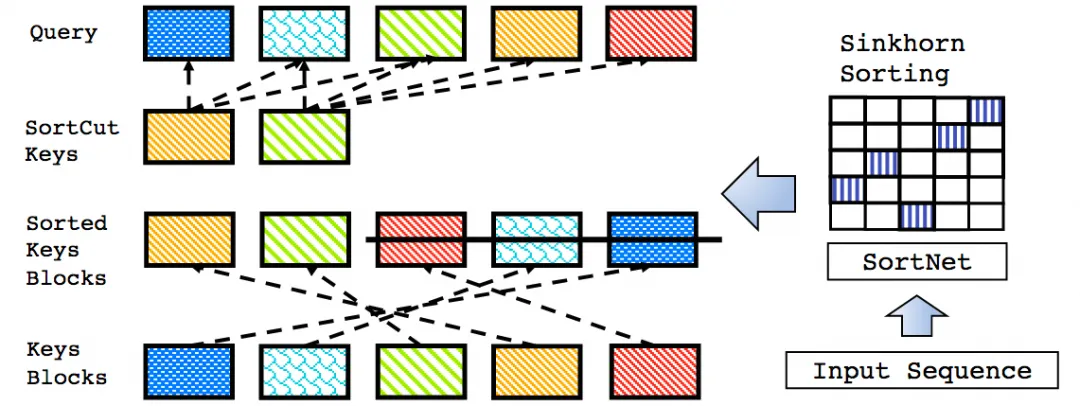
而 mHC 的核心思想正是将残差映射矩阵 $H_l^{res}$ 约束为 双随机矩阵,以此解决 HC 的不稳定问题。
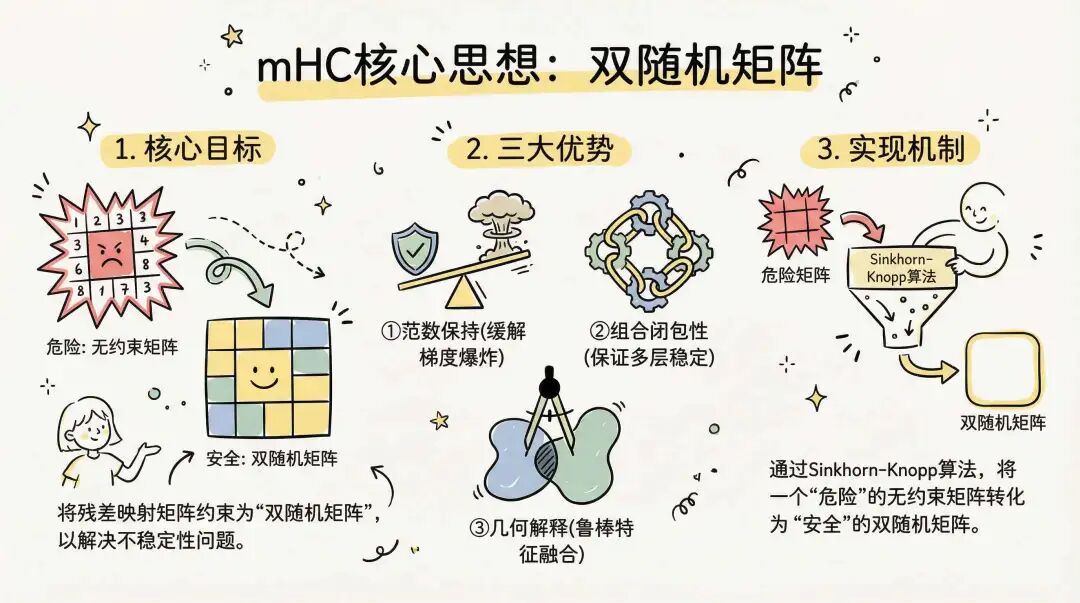
为何选择双随机矩阵?
- 范数保持:双随机矩阵的谱范数不大于 1,这意味着该操作能有效缓解梯度爆炸。
- 组合闭包性:双随机矩阵的乘积仍然是双随机矩阵。这保证了跨多层的复合映射仍然保持稳定性,从而在整个网络深度上维持了信号的稳定传播。
- 几何解释:所有 $n \times n$ 双随机矩阵的集合构成了 Birkhoff 多面体,它是所有 $n \times n$ 置换矩阵的凸包。这意味着 $H_l^{res}$ 的作用可以被解释为对不同残差流进行置换的凸组合,是一种鲁棒的特征融合机制。
实质是:Sinkhorn-Knopp 算法将一个“危险”的无约束矩阵 $\tilde{H}_l^{res}$ 变成了一个“安全”的双随机矩阵 $H_l^{res}$。
1. mHC Overview
1.1 HC如何破坏恒等映射
作者在 Abstract 中提到:HC 通过扩展残差流的宽度和多样化其连接模式,拓展了过去十年间已经无处不在的残差连接范式。尽管这种多样化带来了显著的性能提升,但它从根本上损害了残差连接固有的 恒等映射 属性,从而导致了严重的训练不稳定性和受限的可扩展性,此外还引入了显著的内存访问开销。
首先,我们需要理解标准残差连接是如何实现并受益于恒等映射的。
在一个标准的 ResNet 块中,输出 $x_{l+1}$ 是输入 $x_l$ 和一个非线性变换 $F(x_l)$ 的和:
$x_{l+1} = x_l + F(x_l)$
当我们把这个公式从浅层 $x_\ell$ 递归地展开到深层 $x_L$ 时,会得到:
$x_L = x_\ell + \sum_{i=\ell}^{L-1} F(x_i)$
现在我们来看 HC 的公式。HC 首先将残差流扩展为 $n$ 个并行的流,我们用一个 $n \times C$ 的矩阵 $H_\ell$ 来表示。其单层更新规则为:
$H_{l+1} = H_l + F(H_l H_l^{pre}) H_l^{post} H_l^{res}$
这里的 $H_l^{res}$ 是一个 $n \times n$ 的可学习矩阵。让我们像之前一样,把这个公式从浅层 $H_\ell$ 递归展开到深层 $H_L$。为了简化,我们暂时忽略残差部分,只看主干的传播:
$H_L \approx (\prod_{i=\ell}^{L-1} H_i^{res}) H_\ell$
我们将这个复合映射记为 $\prod_{i=\ell}^{L-1} H_i^{res}$。那么:
$H_L \approx (\prod_{i=\ell}^{L-1} H_i^{res}) H_\ell$
如下图所示,在 ResNet 结构中,来自任意浅层 $\ell$ 的信息,可以通过一条不含任何变换的、纯粹的加法路径,直接传递到任意深层 $L$。这条纯粹的加法路径就是恒等映射。
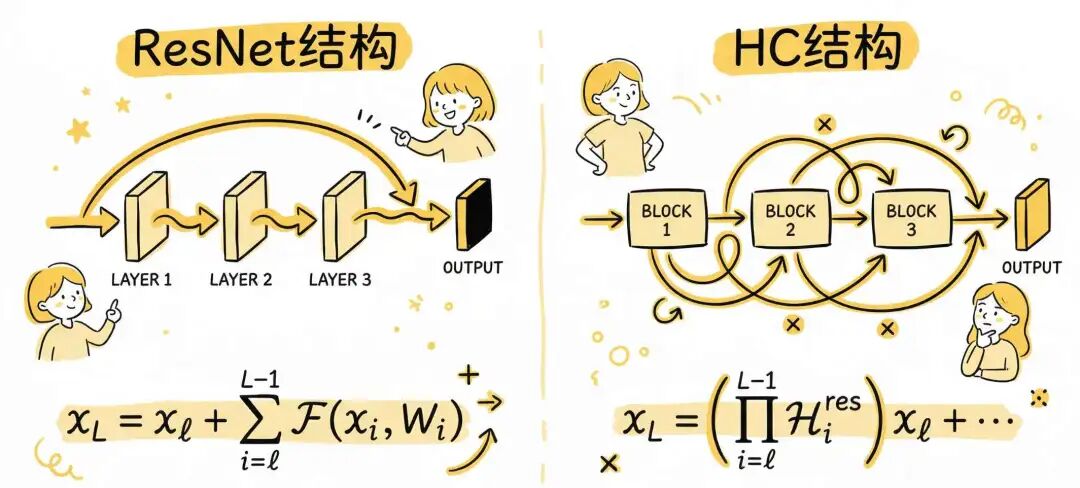
而在 HC 的设计中,$H_l^{res}$ 是一个 无约束的 可学习矩阵。这意味着它的元素可以是任意值,它的性质 (如范数,行列和) 是完全不可控的。矩阵连乘会产生指数级的放大或缩小效应。如果每个 $H_l^{res}$ 的谱范数略大于 1,比如 1.1,那么经过 $L$ 层传播后,复合矩阵的范数可能会增长到 $1.1^L$。当网络很深时,$L$ 很大,这会导致信号的 指数级爆炸。反之,如果范数略小于 1,比如 0.9,就会导致信号的 指数级消失。
1.2 Mainfold Constrained
基于这个问题,DeepSeek 提出了 流形约束超连接。它将 HC 的残差连接空间投影到一个特定的流形上,以恢复恒等映射属性,同时结合了严格的基础设施优化来保证效率。
具体来说,mHC 利用 Sinkhorn-Knopp 算法 将 $H_l^{res}$ 进行熵投影到 Birkhoff 多面体上。这个操作有效地将残差连接矩阵约束在由 双随机矩阵 构成的流形内。由于这些矩阵的行和与列和都等于 1,$H_l^{res}$ 这个操作起到了对输入特征进行凸组合的作用。这一特性促进了一种稳态的信号传播,其中特征均值得以守恒,并且信号范数被严格正则化,有效地减轻了信号消失或爆炸的风险。此外,由于双随机矩阵对于矩阵乘法是闭合的,复合映射 $\prod_{i=\ell}^{L-1} H_i^{res}$ 保持了这种守恒属性。因此,mHC 有效地在任意深度之间维持了恒等映射的稳定性。
另一方面,为了确保效率,mHC 采用了 算子融合 并利用 Tilelang 开发了混合精度算子。此外,通过选择性重计算减轻了内存占用,并在 DualPipe 调度中细致地重叠了通信。当扩展率 $n=4$ 时,mHC 支持规模化训练,并且仅引入了 6.7% 的额外时间开销。
总体来看,整个 Abstract 和 Introduction 指出了 HC 存在的三个重要问题:
- HC 破坏了 “恒等映射”。恒等映射保证了信号和梯度可以无损地在网络中深层传播,是解决深度网络梯度消失/爆炸问题的基石。一旦破坏,信号在逐层传播中可能被无界地放大或衰减。
- 实验中的一些后果:
- 训练不稳定性:理论上的信号衰变/放大直接导致训练过程中的损失尖峰和梯度爆炸。
- 可扩展性受限:这种不稳定性会随着模型深度和规模的增加而被放大,使得 HC 难以应用于真正的大规模模型训练。
- 内存访问开销:扩展的残差流意味着需要从内存中读写更多的数据。在现代计算中,内存带宽往往是瓶颈。HC 虽然计算量增加不多,但其巨大的内存访问成本会严重拖慢实际训练速度。
DeepSeek 的做法是:在算法层面使用了来自数学中微分几何和拓扑学的概念 流形。具体来说,是将连接矩阵 “投影” 到一个具有特定良好性质的流形上。这个投影操作的目的是 “恢复恒等映射属性”,直接对标之前发现的核心问题。这是一种非常优雅且有力的解决方案。在基础设施层面,通过一系列优化,直接回应了 HC 带来的内存访问开销问题。“流形约束” 这个提法非常高明,它将一个工程问题提升到了一个更抽象和普适的数学框架下。
2. 相关工作
这一章对于深度学习中的架构进展从微观设计和宏观设计两个维度进行了分析。
- 微观设计:关注“积木块”本身的设计 (如 Attention, FFN, 卷积核)。
- 宏观设计:关注如何“搭建积木”(层与层之间的连接方式)。
2.1 微观设计
大致阐述了从 CNN 处理结构化信号到 Transformers 的出现确立了 注意力机制 和 前馈网络 作为现代架构的基础构建模块。注意力机制促进了全局信息的传播,而 FFN 则增强了单个特征的表示能力。然后展开介绍了 Attention Block 的演进,例如 MQA/GQA/MLA 等。也阐述了 FFNs 也通过 MoE 范式被推广为稀疏计算,允许在不按比例增加计算成本的情况下实现大规模的参数扩展。
2.2 宏观设计
宏观设计主导了网络的全局拓扑结构,例如 ResNet/DenseNet/FractalNet 等架构分别通过稠密连接和多路径结构来增加拓扑复杂性,以期提升性能。深度层聚合通过在不同深度和分辨率上递归地聚合特征,进一步扩展了这一范式。
然后展开介绍了近期的工作,宏观设计的焦点已经转向 扩展残差流的宽度。Hyper-Connections 引入了可学习的矩阵来调节不同深度特征之间的连接强度;Residual Matrix Transformer 则用一个外积内存矩阵替换了标准的残差流以促进特征存储;MUDDFormer 采用多路动态稠密连接来优化跨层信息流。
紧接着话锋一转,点出了这些结构的问题:它们损害了残差连接固有的 恒等映射属性,从而引入了不稳定性并阻碍了可扩展性。另一部分的问题是,由于特征宽度的扩展,它们也带来了显著的内存访问开销。
最后介绍了 mHC 的区别:在 HC 的基础上将残差连接空间约束在一个特定的流形上以恢复恒等映射属性,同时还结合了基础设施优化来确保效率。这种方法在保持扩展连接所带来的拓扑优势的同时,增强了稳定性和可扩展性。
3. 预备知识
作者在 mHC 论文的第三章介绍了一些预备知识。首先是这篇论文使用的符号体系:
在 HC 的公式中,第 $l$ 层的输入 $x_l$ 被扩展 $n$ 倍,以构建一个隐矩阵 $H_l \in \mathbb{R}^{n \times C}$,这可以被看作是 $n$ 流的残差。这个操作有效地加宽了残差流的宽度。为了控制这个流的读出、写入和更新过程,HC 引入了三个可学习的线性映射:$H_l^{pre} \in \mathbb{R}^{n \times 1}$, $H_l^{post} \in \mathbb{R}^{1 \times n}$, $H_l^{res} \in \mathbb{R}^{n \times n}$。这些映射修改了标准残差连接公式 $x_{l+1} = x_l + F(x_l)$,得到了如下公式:
$H_{l+1} = H_l + F(H_l H_l^{pre}) H_l^{post} H_l^{res}$
在 HC 的公式中,可学习的映射由两部分系数组成:依赖于输入的部分和全局的部分,分别被称为动态映射和静态映射。形式上,HC 如下计算这些系数:
$[H_l^{pre}, H_l^{post}, H_l^{res}] = g_l^{dyn} \cdot \text{RMSNorm}(x_l \theta_l^{dyn}) + g_l^{sta} \cdot b_l^{sta}$
其中 RMSNorm(·) 应用于最后一个维度,标量 $g_l^{dyn}$ 和 $g_l^{sta}$ 是被初始化为很小值的可学习门控因子。
- 动态映射通过由 $\theta_l^{dyn}$ 和 $\theta_l^{sta}$ 参数化的线性投影导出
- 静态映射则由可学习的偏置 $b_l^{dyn}$ 和 $b_l^{sta}$ 表示
值得注意的是,引入这些映射 $H_l^{pre}$ 和 $H_l^{post}$ 所带来的计算开销可以忽略不计,因为典型的扩展率 $n$ (例如 4) 远小于输入维度 $C$。通过这种设计,HC 有效地将残差流的信息容量与模型的计算复杂度 (FLOPs) 解耦。因此,HC 通过调整残差流宽度,为模型扩展提供了一条新的途径。
尽管 HC 需要三个映射来管理残差流和层输入之间的维度不匹配,但下表中展示的 HC 组件消融研究的实验表明,残差映射 $H_l^{res}$ 产生了最显著的性能增益。这一发现强调了在残差流内部进行有效信息交换的至关重要的作用。
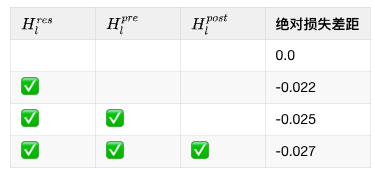
注:当某个特定映射 ($H_l^{pre}$, $H_l^{post}$, 或 $H_l^{res}$) 被禁用时,采用一个固定的映射来保持维度一致性。
3.1 数值稳定性分析
尽管残差映射 $H_l^{res}$ 对性能至关重要,但其顺序应用对数值稳定性构成了重大风险。正如公式 $H_L \approx (\prod_{i=\ell}^{L-1} H_i^{res}) H_\ell$ 所示,当 HC 扩展到多层时,从层 $\ell$ 到 $L$ 的有效信号传播由复合映射 $\prod_{i=\ell}^{L-1} H_i^{res}$ 控制。由于可学习映射 $H_l^{res}$ 是无约束的,这个复合映射不可避免地会偏离恒等映射。因此,信号幅度在正向传播和反向传播中都容易发生爆炸或消失。这种现象破坏了残差学习依赖于无阻碍信号流的基本前提,从而在更深或更大规模的模型中破坏了训练过程的稳定性。
经验证据支持了这一分析。作者在大规模实验中观察到不稳定的损失行为,如图所示。以 mHC 为基线,HC 在约 12k 步时表现出意外的损失飙升,这与梯度范数的不稳定性高度相关。
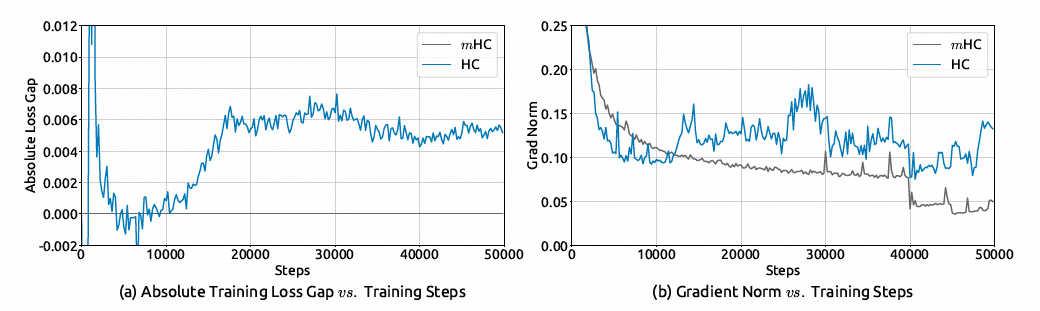
此外,对 $H_l^{res}$ 的分析验证了这种不稳定性的机理。为了量化复合映射 $\prod_{i=\ell}^{L-1} H_i^{res}$ 如何沿残差流放大信号,作者使用了两个指标:
- 基于复合映射的 行和的最大绝对值,捕捉前向传播中的最坏情况扩展。
- 基于 列和的最大绝对值,对应于反向传播。
并将这些指标称为复合映射的 Amax 增益幅度。如下图 (b) 所示,Amax 增益幅度产生了极值,峰值达到 3000,巨大差异证实了残差流爆炸的存在。
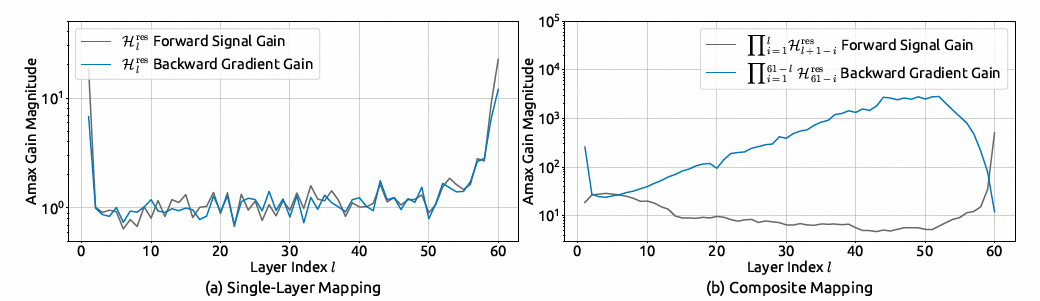
Amax增益幅度分析:
作者定义了一个非常巧妙的指标: Amax增益幅度。
- 对于一个矩阵 $M$,前向传播中的 Amax增益幅度是 $\max_i \sum_j |M_{ij}|$,即最大绝对行和。
- 对于一个矩阵 $M$,反向传播中的 Amax增益幅度是 $\max_j \sum_i |M_{ij}|$,即最大绝对列和。
为什么Forward是行和?
考虑一个输入向量 $x$,输出 $y = Mx$。输出的第 $i$ 个分量是 $y_i = \sum_j M_{ij} x_j$。如果我们假设输入向量 $x$ 的所有元素绝对值最多为 $c$,那么 $|y_i| \le c \sum_j |M_{ij}|$。因此,行和 $\sum_j |M_{ij}|$ 直接决定了输入信号在传播到输出的第 $i$ 个分量时可能被放大的最大倍数。最大绝对行和就代表了在所有输出分量中最坏情况下的放大因子。
为什么Backward是列和?
考虑反向传播,损失 $L$ 对输入 $x$ 的梯度是 $\frac{\partial L}{\partial x} = M^T \frac{\partial L}{\partial y}$。根据不等式:如果假设上游梯度向量的绝对值最大为 $c‘$,那么 $|\frac{\partial L}{\partial x_j}| \le c' \sum_i |M_{ij}|$。因此,列和 $\sum_i |M_{ij}|$ 直接决定了上游梯度在反向传播到输入第 $j$ 个分量时可能被放大的最大倍数。最大绝对列和就代表了在所有输入分量中最坏情况下的梯度放大因子。
对上图的展开分析
上图中的 (a) 展示了单个 $H_l^{res}$ 矩阵的增益幅度。即使是单个矩阵,其 Amax 增益幅度也已经偏离了 1,大部分值在 1 到 2 之间,有些甚至接近 10。这表明 HC 的可学习映射在每一层都引入了微小但确定的放大效应。虽然单层的放大看起来不严重,但这正是问题的根源,它为后续的指数级爆炸埋下了伏笔。
图 (b) 是整篇论文中最具说服力的部分。它展示了多个 $H_l^{res}$ 矩阵 连乘 后的复合效应。随着层数的增加,复合映射的增益幅度呈指数级增长。注意 y 轴是对数尺度,曲线近似线性就意味着指数增长。在网络的中后段,Amax 增益幅度达到了 $10^3$ 到 $10^4$ 的量级,论文中提到的“峰值达到 3000”就来源于此。这张图清晰地可视化了引言和第三章中描述的理论问题:无约束矩阵的连乘导致信号/梯度的指数级爆炸。
3.2 系统开销
虽然由于额外映射的线性特性,HC 的计算复杂度仍然可控,但系统级开销带来了不可忽略的挑战,特别就是关于访问内存的开销。
下表分析了由 $n$ 流残差设计在单个残差层中引入的每个 token 的内存访问开销。
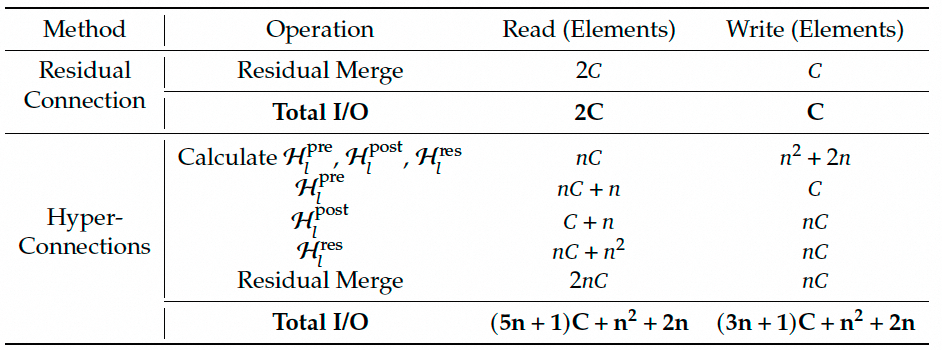
分析显示,HC 将内存访问成本增加了大约与 $n$ 成正比的一个因子。如果没有融合算子的缓解,这种过度的 I/O 需求会显著降低训练吞吐量。
此外,由于 $H_l^{pre}$ 和 $H_l^{post}$ 涉及可学习参数,它们的反向传播需要中间激活值。这导致 GPU 内存占用的巨大增加,通常需要梯度检查点来维持可行的内存使用。
此外,HC 在流水线并行中需要 $n$ 倍的通信成本,导致更大的 bubbles 和训练吞吐量的下降。
量化分析:标准残差连接的总 I/O 约为 $3C$。HC 的总 I/O 约为 $(8n+2)C + 2n^2 + 4n$。当 $n=4$ 时,I/O 成本大约是原来的 10 倍以上,这是一个巨大的开销。
4. mHC算法和实现
4.1 流形约束超连接
mHC 从 ResNet 中的恒等映射原理中汲取灵感,核心前提是将残差映射 $H_l^{res}$ 约束在一个特定的流形上。原始的恒等映射通过强制 $H_l^{res} = I$ (单位矩阵) 来确保稳定性,但它从根本上排除了残差流内部的信息交换,而这对于最大化多流架构的潜力至关重要。因此作者建议将残差映射投影到一个既能维持跨层信号传播稳定性,又能促进残差流之间相互作用以保持模型表达能力的流形上。
为此,作者将 $H_l^{res}$ 限制为一个 双随机矩阵,其具有非负的元素,并且行和与列和均为 1。形式上,令 $\mathcal{M}^{res}$ 表示双随机矩阵的流形 (也被称为 Birkhoff 多面体)。将 $H_l^{res}$ 约束为 $\mathcal{M}^{res}$,定义为:
$\mathcal{M}^{res} = \{ H \in \mathbb{R}^{n \times n} \mid H_{ij} \ge 0, \ H \mathbf{1} = \mathbf{1}, \ \mathbf{1}^T H = \mathbf{1}^T \}$
其中 $\mathbf{1}$ 代表全 1 的 $n$ 维向量。值得注意的是,当 $n=1$ 时,双随机条件退化为标量 1,从而恢复了原始的恒等映射。
然后作者展开讲了一下选择双随机矩阵流形的理论依据:
- 范数保持:双随机矩阵的谱范数被 1 所界定 (即,$\|H\|_2 \le 1$)。这意味着该可学习映射是 非扩张的,有效地缓解了梯度爆炸问题。
- 组合闭包性:双随机矩阵的集合在矩阵乘法下是封闭的。这确保了跨多层的复合残差映射 $\prod_{i=\ell}^{L-1} H_i^{res}$ 仍然是双随机的,从而在模型的整个深度上保持了稳定性。
- 通过 Birkhoff 多面体的几何解释:$\mathcal{M}^{res}$ 集合构成了 Birkhoff 多面体,它是置换矩阵集合的凸包。这提供了一个清晰的几何解释:残差映射扮演着 置换的凸组合 的角色。从数学上讲,重复应用此类矩阵倾向于单调地增加跨流信息的混合,有效地充当了一种鲁棒的特征融合机制。
此外,对输入映射 $H_l^{pre}$ 和输出映射 $H_l^{post}$ 施加了非负性约束。这种约束防止了由正负系数组合引起的信号抵消,这也可以被视为一种特殊的流形投影。
双随机矩阵与 Birkhoff 多面体
一个 $n \times n$ 的实数矩阵 $H$ 被称为双随机矩阵,如果满足:1) 非负性;2) 行和为 1;3) 列和为 1。Birkhoff 多面体 $\mathcal{B}_n$ 就是所有满足上述条件的 $n \times n$ 矩阵所构成的集合,它是一个凸多面体。
Birkhoff-von Neumann 定理指出,Birkhoff 多面体 $\mathcal{B}_n$ 是所有 $n!$ 个 $n \times n$ 置换矩阵的 凸包。换句话说,$\mathcal{B}_n$ 的顶点恰好是 $n!$ 个 $n \times n$ 的置换矩阵。也就是说,如果 $H$ 是一个双随机矩阵,那么存在系数 $\lambda_k \ge 0, \sum_k \lambda_k = 1$ 和置换矩阵 $P_k$ 使得:$H = \sum_k \lambda_k P_k$。
这对 mHC 的流形约束有什么作用?
对 $H_l^{res}$ 操作,本质是“加权平均的洗牌”。对输入 $H_l$ 应用 $H_l^{res}$ 操作,即计算 $H_l H_l^{res}$,等价于:$H_l H_l^{res} = \sum_k \lambda_k (H_l P_k)$。这个式子清晰地表明,mHC 的残差更新过程,是对输入 $H_l$ 进行所有可能的 $n!$ 种“洗牌”(置换)操作,然后将这些“洗牌”后的结果进行加权平均。“加权平均”是一种典型的混合操作,天然地不具备放大信号的能力,这从几何上保证了信号的稳定性。
论文中提到 mHC 是一个“鲁棒的特征融合机制”。这里的鲁棒性就来源于 Birkhoff 多面体的凸性。无论网络学习到的 $H_l^{res}$ 在多面体内部的哪个位置,它都逃不出“加权平均洗牌”这个范畴,其行为是可预测和有界的。
另一个重要性质是 乘法下的闭包性:两个双随机矩阵的乘积仍然是一个双随机矩阵。这是保证 mHC 可扩展到任意深度 的关键。考虑跨多层的复合映射 $\prod_{i=\ell}^{L-1} H_i^{res}$。由于每个 $H_i^{res}$ 都是 Birkhoff 多面体中的一个点,它们的乘积也必定是 Birkhoff 多面体中的一个点。这意味着,无论网络有多深,从任意浅层到任意深层的净残差传播效应,始终等效于单个双随机矩阵的操作。稳定性不会因为深度的增加而退化,完美解决了 HC 的指数累积爆炸问题。
通过 Birkhoff 多面体的性质,我们可以将 mHC 的流形约束理解为:
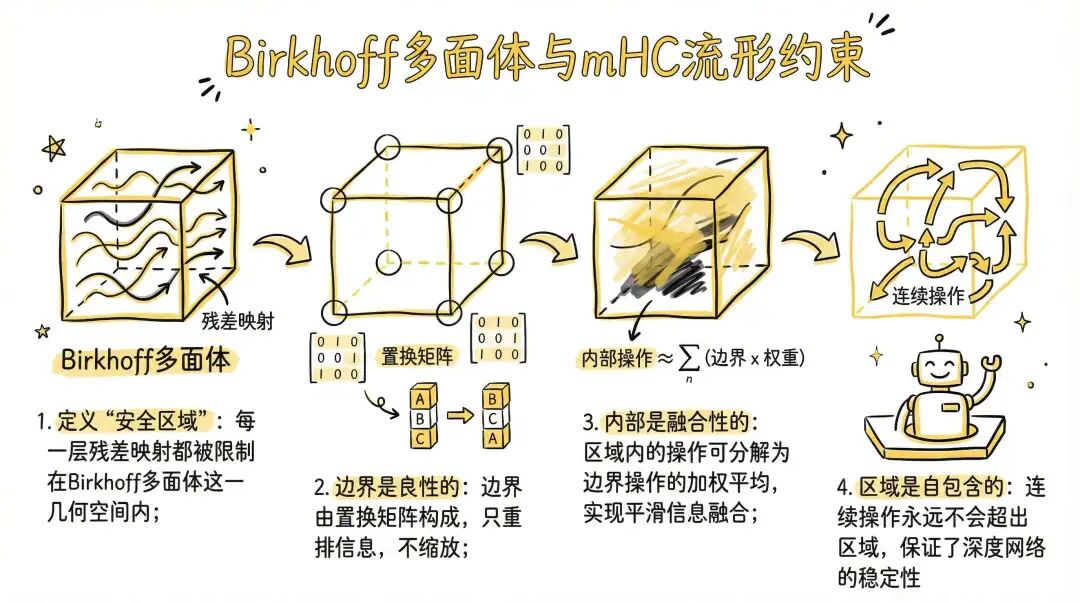
4.2 参数化与流形投影
在本节中,作者详细介绍 mHC 中 $H_l^{pre}$, $H_l^{post}$ 和 $H_l^{res}$ 的计算过程。
给定第 $l$ 层的输入隐矩阵 $H_l$,首先将其展平为一个向量 $\bar{x}_l = \text{flatten}(H_l) \in \mathbb{R}^{1 \times nC}$ 以保留完整的上下文信息。
然后,遵循原始 HC 的公式来获得动态映射和静态映射,如下所示:
$[\tilde{H}_l^{pre}, \tilde{H}_l^{post}, \tilde{H}_l^{res}] = g_l^{dyn} \cdot (\bar{x}_l \phi_l^{dyn}) + g_l^{sta} \cdot b_l^{sta}$
其中 $\phi_l^{dyn}$ 和 $b_l^{sta}$ 是用于动态映射的线性投影,而 $\text{reshape}_{(n)}$ 是一个从 $\mathbb{R}^{1 \times (n + n + n^2)}$ 到 $(\mathbb{R}^{n \times 1}, \mathbb{R}^{1 \times n}, \mathbb{R}^{n \times n})$ 的 reshape 函数。
对 $\bar{x}_l$ 的处理:将 $H_l$ 的多流输入矩阵展平成一个长向量。这是一个关键的改进。在原始 HC 的公式中,输入是 $x_l$,这通常意味着对每个流 (每一行) 单独做 Norm 来生成映射矩阵。而 mHC 通过 $\bar{x}_l$ 保留了所有流的全部信息,将它们拼接在一起。这使得后续的线性投影 $\phi_l^{dyn}$ 可以访问到所有流的完整上下文,从而能够学习到更复杂的流间依赖关系来生成映射矩阵。这种全局上下文感知是原始 HC 所不具备的。
动态映射与静态映射:
- 动态部分:$\bar{x}_l \phi_l^{dyn}$。这是一个标准的线性层,使得生成的映射矩阵是输入依赖的,能够根据不同的输入 token 动态调整连接模式。
- 静态部分:$b_l^{sta}$。这是一个可学习的偏置项,代表了独立于输入的全局连接偏好。
- 门控因子:$g_l^{dyn}, g_l^{sta}$。在训练初期通过小值初始化,起到稳定训练的作用,使得初始的映射矩阵接近于静态偏置 $b_l^{sta}$。
然后,最终的约束映射通过以下方式获得:
$H_l^{pre} = \sigma(\tilde{H}_l^{pre})$
$H_l^{post} = 2\sigma(\tilde{H}_l^{post})$
$H_l^{res} = \text{Sinkhorn-Knopp}(\exp(\tilde{H}_l^{res}))$
其中 $\sigma$ 表示 Sigmoid 函数。$\text{Sinkhorn-Knopp}$ 算子首先通过一个指数算子使所有元素为正,然后执行一个交替重新缩放行和列以使它们的和为 1 的迭代归一化过程。
具体来说,给定一个正矩阵 $M^{(0)} = \exp(\tilde{H}_l^{res})$ 作为起点,归一化迭代过程如下:
$M^{(2t+1)} = M^{(2t)} / (M^{(2t)} \mathbf{1}) \quad \text{(行归一化)}$
$M^{(2t+2)} = M^{(2t+1)} / (\mathbf{1}^T M^{(2t+1)}) \quad \text{(列归一化)}$
其中 $/$ 表示逐元素除法。当 $t \to \infty$ 时,这个过程收敛到一个双随机矩阵 $H_l^{res}$。在实验中,作者选择迭代 20 次 ($t=10$)。
约束施加阶段:
这个阶段是 mHC 的核心创新所在,它将阶段一生成的“原始”矩阵投影到目标流形上。
- $H_l^{pre}$ 和 $H_l^{post}$ 的约束:原始 HC 使用 tanh,值域为 (-1,1),可能产生负数。mHC 中,$H_l^{pre}$ 使用 Sigmoid 函数,结果在 (0, 1) 之间,施加了非负性约束,意味着从多流到单流的聚合是一个加权平均或加权求和,避免了负权重导致的信号抵消。$H_l^{post}$ 同样使用 Sigmoid 但乘以 2,使得元素范围在 (0, 2) 之间,同样施加了非负性,但在将特征写回时适度放大信号。
- Sinkhorn-Knopp 算法:该算法最初由 Richard Sinkhorn 和 Paul Knopp 研究,解决如何将一个正矩阵通过行列交替缩放变为双随机矩阵的问题。其核心思想非常直观:既然不能一步到位,那就轮流来。它通过迭代过程,交替地满足行约束和列约束。
与最优传输的联系
最优传输问题:想象你有两堆沙子 (两个概率分布 $\mathbf{a}$ 和 $\mathbf{b}$),你想以最小的“搬运成本”将第一堆沙子变成第二堆的样子。“搬运计划”就是一个矩阵 $P$。离散形式的 OT 问题可以写成一个线性规划。
在 mHC 中,将矩阵 $\tilde{H}_l^{res}$ 投影到双随机流形上,相当于求解一个特殊的最优传输问题:目标分布 $\mathbf{a}$ 和 $\mathbf{b}$ 都是均匀分布,即 $\mathbf{1}/n$;成本矩阵 $C$ 就是 $-\tilde{H}_l^{res}$ (最大化 $\langle P, \tilde{H}_l^{res} \rangle$ 等价于最小化 $\langle P, -\tilde{H}_l^{res} \rangle$)。为了解决计算复杂度高的问题,Marco Cuturi 提出了加入 熵正则化项 的 Sinkhorn 算法。而求解该问题的过程,恰好就是 Sinkhorn-Knopp 算法!因此,mHC 中使用的 Sinkhorn-Knopp 算法,实际上是在高效地求解一个熵正则化的最优传输问题,其目的是找到一个与原始生成矩阵 $\tilde{H}_l^{res}$ “最相似” 的双随机矩阵。
另一方面,Sinkhorn-Knopp 算法还有两个对工程实现很重要的优势:
- 可微分:尽管是一个迭代算法,但它的每一步操作都是可微的,可以嵌入到神经网络中进行端到端训练。
- 高效并行:核心操作是矩阵-向量乘、求和、逐元素除法等,在 GPU 上可以高度并行化。
4.3 mHC工程实现
这一节阐述了在工程实现上的细节。通过严格的优化,作者在大型模型中实现了 mHC (当 $n=4$ 时),其边际训练开销仅为 6.7%。
4.3.1 算子融合
首先观察到 mHC 中的 RMSNorm 在处理高维隐藏状态 $H_l$ 时会带来显著的延迟,因此将除以范数的操作重新排序到矩阵乘法之后。这种优化在保持数学等价性的同时提高了效率。

基于公式 (10) 到 (13) 中详述的输入和参数,实现了三个专门的 mHC 算子来计算 $\tilde{H}_l^{pre}$, $\tilde{H}_l^{post}$ 和 $\tilde{H}_l^{res}$。在这些算子中,偏置和线性投影被合并,RMSNorm 的权重也被吸收到参数中。
公式 (14) 到 (15):作者开发了一个统一的算子,它融合了对 $\bar{x}_l$ 的两次扫描 (一次用于矩阵乘法,一次用于计算范数),利用矩阵乘法单元来最大化内存带宽利用率。反向传播 (包含两次矩阵乘法) 同样被合并成一个单一算子,消除了对 $\bar{x}_l$ 的重复加载。这两个算子都具有一个精细调优的流水线 (加载,类型转换,计算,存储) 来高效地处理混合精度。
RMSNorm 优化详解:
标准的 RMSNorm 计算需要完整地读取两遍高维向量 $\bar{x}_l$,导致 Memory Bound 的操作成为性能瓶颈。作者提出的优化是重新排序操作:
原始计算:$\bar{x}_l‘ = \frac{\bar{x}_l}{\text{RMS}(\bar{x}_l)} \cdot \text{gain} \quad \text{然后计算} \quad \bar{x}_l‘ \phi_l^{dyn}$
优化后:先计算未归一化的矩阵乘法结果 $\text{IntermediateResult} = \bar{x}_l \phi_l^{dyn}$,同时计算 $\bar{x}_l$ 的 L2 范数所需的分母 $r = \|\bar{x}_l\|_2 / \sqrt{nC}$。这样,对 $\bar{x}_l$ 的访存从两次减少到了一次。最后,计算最终结果 $\bar{x}_l‘ \phi_l^{dyn} = \text{IntermediateResult} / r$。这一步是在较小的 IntermediateResult 张量上进行的,开销更小。
公式 (16) 到 (18):这些在小系数上进行的轻量级操作被融合成一个单一算子,显著减少了算子启动开销。
公式 (19):将 Sinkhorn-Knopp 迭代实现在一个单一算子内。对于反向传播,推导了一个自定义的反向算子,它在芯片上重计算中间结果并遍历整个迭代过程。
Sinkhorn-Knopp 算子优化:
- Forward:朴素实现会启动大量 kernel,迭代 20 次意味着至少 40 次 kernel 启动和 40 次对整个矩阵的 DRAM 读写,开销巨大。优化后,用一个 kernel 在多个 SM 的共享内存中完成所有迭代,极大减少了 kernel launch 和全局内存访问。
- Backward:没有依赖 PyTorch 的自动微分来保存所有中间结果,而是手动推导了整个 Sinkhorn-Knopp 过程的梯度公式,并将其也实现为一个单一、高效的 CUDA Kernel。在反向传播时,只需在片上内存中重计算前向的中间变量 (如每次迭代前的矩阵、列和、行和),然后应用链式法则逐层回传梯度,避免了将大量中间结果保存到全局显存。
使用上述算子派生出的系数,引入了两个额外的算子来应用这些映射:一个用于 $h_0 = H_l H_l^{pre}$ (应用 pre 映射),另一个用于 $H_{l+1} = H_l + \tilde{h}_l H_l^{post} H_l^{res}$ (应用 post 和 res 映射)。通过将 $H_l^{post}$ 和 $H_l^{res}$ 的应用与残差合并操作相融合,将读取的元素数量从 $3nC$ 减少到 $2nC$,将写入的元素数量从 $2nC$ 减少到 $nC$。
值得注意的是,大部分算子 (不包括公式 (14) 到 (15)) 都采用 TileLang 高效地实现,简化了具有复杂计算过程的算子的实现,并允许以最小的工程量充分利用内存带宽。
4.3.2 Recomputing
mHC 将残差流从 $C$ 维扩展到 $nC$ 维。在标准训练中,为了反向传播,前向的所有激活值都需要保存,这会导致内存开销激增 (当 $n=4$ 时,是标准 Transformer 的 4 倍)。为了缓解这一点,mHC 在前向传播后丢弃 mHC 算子的中间激活值,并在反向传播中通过重新执行 mHC 算子来即时重算它们。
具体流程:
- 前向传播:对于一个由 $m$ 层构成的块,只保存块的第一个输入 $H_{\ell}$。在块内部,中间激活值都不保存。
- 反向传播:当梯度反传到这个块的末端时,为了计算对块内权重的梯度,需要块内每一层的输入。此时,从保存的 $H_{\ell}$ 开始,重新执行一次这个块的前向计算 (只计算 mHC 部分和 $h_0$ 的输入,不需要完整计算 Transformer 层),从而得到所有需要的中间激活值,然后再执行真正的反向计算。
在流水线并行中,重计算的边界需要与流水线阶段同步,因为下一个阶段的 GPU 没有上一个阶段的权重和输入,无法进行跨阶段重计算。作者观察到理论最优值 $m$ 通常与每个流水线阶段的层数相符,因此选择将重计算的边界与流水线阶段同步。
4.3.3 流水线排布
扩展 DualPipe 以促进在流水线阶段边界处更好地重叠通信和计算。

值得注意的是,为了防止阻塞通信流,作者在一个专用的高优先级计算流上执行 MLP (即 FFN) 层的反向传播算子。另一方面还进一步避免在 Attention 层中的长耗时操作上使用持久化算子,从而防止长时间的停顿。这种设计使得被重叠的 Attention 计算可以被抢占,从而允许灵活的调度,同时保持计算设备处理单元的高利用率。此外,重计算过程与流水线通信依赖是解耦的,因为每个阶段的初始激活值 $H_{\ell}$ 已经被缓存在本地了。
5. 实验
5.1 Setup
设置了三个明确的比较组:baseline, HC, mHC。
baseline:标准的、没有使用任何超连接技术的模型,作为衡量绝对收益的标尺。HC:mHC 要直接挑战和改进的对象。mHC:本文提出的方法。
为了公平比较,HC 和 mHC 都使用了相同的扩展率 $n=4$。模型架构基于 DeepSeek-V3 的 MoE 架构,在复杂系统上验证 mHC 的有效性更能体现其鲁棒性和通用性。
评估维度:
- 核心性能与效率:采用一个 27B 模型,在计算最优的设定下进行,验证 mHC 的核心性能。
- 可扩展性:通过 3B, 9B, 27B 三种规模的模型,观察 mHC 的优势随模型规模变化的趋势。
- Token 扩展行为:在一个固定的 1T token 语料库上训练一个单独的 3B 模型进行研究。
5.2 主要结果
首先在 27B 模型上展示主要结果,评估集中在下游基准测试性能和训练过程中的系统效率。
如图所示,HC、mHC 和基线模型的训练损失曲线证实了关于 HC 数值不稳定性的分析。
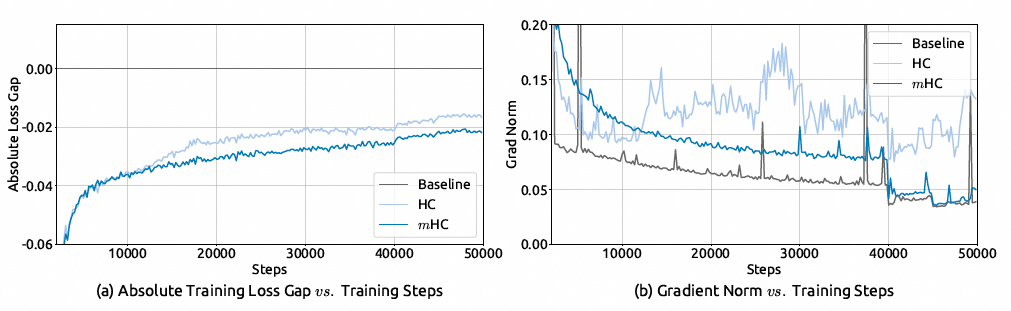
具体来说,HC 在大约 12k 步时遭遇了 Loss 尖峰,这迫使我们手动降低学习率以恢复训练。相比之下,mHC 和基线模型都表现出平滑且稳定的训练动态。这一观察结果强调了 mHC 所施加的流形约束在缓解 HC 固有的传播不稳定性方面的有效性。
然后进一步评估了最终检查点在一系列下游任务上的性能。如表所示,mHC 在所有基准测试中始终优于 HC 和基线模型:

5.3 Scaling
通过在不同模型尺寸和数据量下进行训练,来研究 mHC 的可扩展性。
Compute Scaling
首先通过在 3B, 9B 和 27B 模型上进行训练,来研究 mHC 在不同计算规模下的性能趋势。如图所示,即使在更高的计算预算下,mHC 的性能优势也能被稳健地保持,仅表现出轻微的衰减。
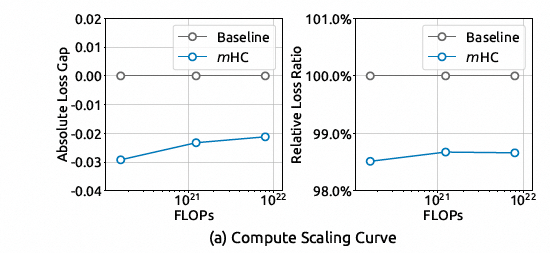
Data Scaling
此外,我们在下图中考察了单次运行中的动态变化,该图展示了 3B 模型上的 Token Scaling 曲线。综合来看,这些发现验证了 mHC 在超大规模场景下的有效性。
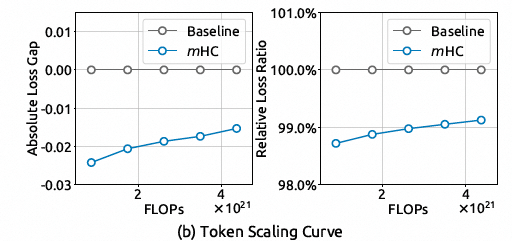
然后注意到一句话:这一结论也得到了我们内部大规模训练实验的进一步证实。
5.4 稳定性分析
下图展示了 mHC 的传播稳定性。理想情况下,单层映射满足双随机约束,这意味着前向信号增益和后向梯度增益都应等于 1。然而,在实际实现中,使用 Sinkhorn-Knopp 算法必须限制迭代次数以保证计算效率。算法上使用 20 次迭代来获得一个近似解。
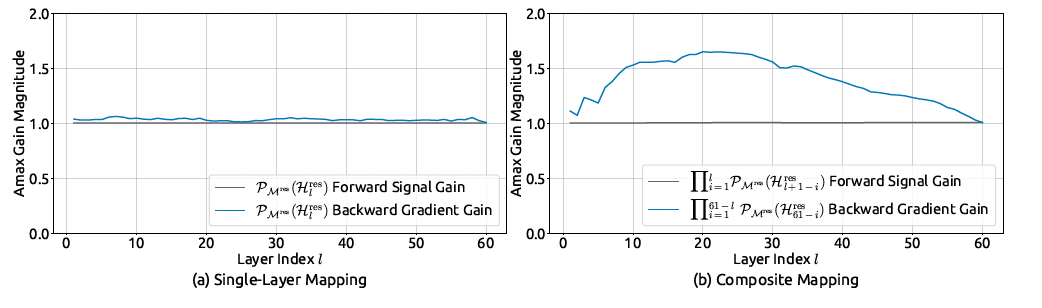
因此,如图 (a) 所示,后向梯度增益会与 1 有轻微的偏差。在图 (b) 所示的复合映射情况下,偏差有所增加但仍然是有界的,最大值达到了约 1.6。值得注意的是,与 HC 中接近 3000 的最大增益幅度相比,mHC 将其显著降低了三个数量级。这些结果表明,与 HC 相比,mHC 极大地增强了传播稳定性,确保了稳定的前向信号和后向梯度流。
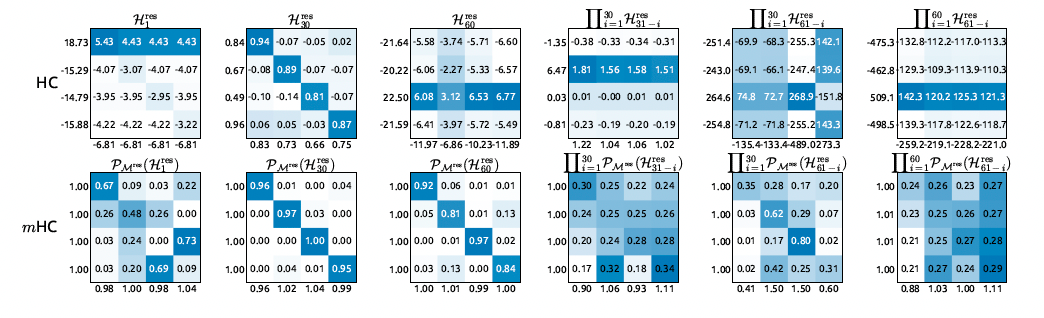
此外,下图展示了代表性的映射矩阵。我们观察到,对于 HC,当最大增益很大时,其他值也往往很大,这表明所有传播路径上都存在普遍的不稳定性。相比之下,mHC 始终产生稳定的结果。
6. 结论和展望
作者认为,尽管像“超连接” (HC) 那样扩展残差流的宽度和多样化连接方式可以带来性能增益,但这些连接的无约束特性会导致信号发散。这种破坏损害了信号能量在跨层传递时的守恒性,引发了训练不稳定性,并阻碍了深度网络的可扩展性。
为应对这些挑战,引入了“流形约束超连接” (mHC),这是一个将残差连接空间投影到特定流形上的通用框架。通过使用 Sinkhorn-Knopp 算法对残差映射强制施加双随机约束,mHC 将信号传播转化为特征的凸组合。实验结果证实,mHC 有效地恢复了恒等映射的特性,实现了稳定的大规模训练,并展现出相比传统 HC 更优越的可扩展性。至关重要的是,通过高效的底层基础设施级优化,mHC 在提供这些改进的同时,只带来了可忽略的计算开销。
作为 HC 范式的一个广义扩展,mHC 为未来的研究开辟了几个有前景的方向。尽管本项工作利用双随机矩阵来确保稳定性,但该框架同样支持探索为特定学习目标量身定制的、多样化的流形约束。作者预期,对不同几何约束的进一步研究可能会催生出新的方法,从而更好地优化模型的可塑性与稳定性之间的权衡。此外,我们希望 mHC 能够重新激发社区对宏观架构设计的兴趣。通过加深对拓扑结构如何影响优化和表示学习的理解,mHC 将有助于解决当前的局限性,并可能为下一代基础架构的演进指明新的道路。
总结与思考
对于 mHC,部分同学的理解可能停留在“HC 扩展了残差流,mHC 增加了稳定性”的层面,或者 Infra 同学只关注 Sinkhorn 算法的行列迭代。但实际上,从流形的视角探索更多约束是极具价值的。正如论文所言,对不同几何约束的进一步研究可能会催生出新的方法。例如,是否可以在整个模型上对 Attention 也施加流形约束?或者针对不同任务设计不同的可组合 Attention 流形约束?这些都是值得探讨的方向。
另一方面,我一直坚信的一点是:这一次人工智能革命的数学基础是范畴论、代数拓扑、代数几何这些二十世纪的数学第一次登上商用计算的舞台。然而这方面的进展和国内一些前沿实验室的专注度似乎还不够。DeepSeek 这一次很巧妙地利用了双随机矩阵的性质来构建 mHC,很好地运用了 Birkhoff 多面体的性质和 Birkhoff-von Neumann 定理。
从最优传输的视角,在 mHC 中,将矩阵 $\tilde{H}_l^{res}$ 投影到双随机流形上,相当于求解一个特殊的最优传输问题(目标分布为均匀分布)。然后利用了 Optimal Transport 中的 Sinkhorn-Knopp 算法,同时利用了它可微分、可并行的特性。整体的计算开销又通过基础设施的优化压缩到了一个很低的代价。整个工作非常干净、纯粹,而又非常细致。
个人觉得其最大的价值还是在于将新的数学工具和视角引入到 模型优化 领域,从而获得全新的问题解决方案。对于这类前沿技术的深入探讨和交流,欢迎关注 云栈社区,一个专注于技术深度分享的开发者社区。
参考资料
[1] mHC: Manifold-Constrained Hyper-Connections: https://arxiv.org/pdf/2512.24880
[2] Hyper-Connection: https://arxiv.org/pdf/2409.19606
[3] 都2025年了,我不允许你还在用残差连接!: https://zhuanlan.zhihu.com/p/20810468231
[4] Virtual Width Networks: https://arxiv.org/pdf/2511.11238
[5] Nerve in Category Theory: https://en.wikipedia.org/wiki/Nerve_(category_theory)
[6] CONCERNING NONNEGATIVE MATRICES AND DOUBLY STOCHASTIC MATRICES: https://msp.org/pjm/1967/21-2/pjm-v21-n2-p14-s.pdf