PPO算法细节
上节提出的 V 和 A 互相套娃表述有误。这不是死循环(套娃),而是一个“自举(Bootstrapping)”的过程。
关键在于区分 时间步 和 网络状态 :
- 计算
A 时,使用的是 采样阶段冻结的旧价值网络 进行 预测。
- 更新价值网络时,使用的是 上述计算出的“回报(Return)”作为标签(Label/Target) ,来训练 当前的价值网络。
下面将分三个部分详细解析:解开“套娃”误区、价值网络更新机制、以及不省略任何符号的PPO完整训练流程。
第一部分:解开“套娃”误区——谁是新策略,谁是旧策略?
提到的矛盾点在于:
- 求
A 需要 V。
- 求
V 的更新目标又需要 A。
这里的 V 其实指代了两个不同的东西:
1. 用于“预测”的 V (Old Critic)
在PPO的 采样阶段(Rollout) 结束后,我们拥有了一批数据。此时我们立刻使用当前的价值网络(参数为 θ_v)去计算每个状态的价值 V_θ_v(s)。
- 这个值是 固定 的,不再是一个变量,而是一个标量数值。
- 我们用这个数值和奖励
r 结合,计算出 A。此时 A 也成为了一个固定的标量数值。
2. 用于“拟合”的 V (Current Critic)
在PPO的 优化阶段(Update) ,我们希望优化价值网络的新参数 θ_v'。
- 我们的目标是让新网络输出的
V_θ_v'(s) 尽可能接近真实回报。
- 真实回报怎么算?我们就用刚才算出来的
A 作为 Ground Truth(目标值)。
- 关键点:目标值是用旧参数算出来的(固定值),而我们在优化的是新参数。
总结:是用“旧参数预测出的价值”来构建“目标”,指导“新参数”的更新。这就是强化学习中的 TD-Learning(时序差分)思想。
第二部分:价值网络(Critic)是如何更新的?
在LLM的PPO中,通常有一个独立的Critic模型(或者与Actor共享部分参数),它的作用是估计当前Prompt和已生成Token序列(State)的预期收益。
1. 目标值(Target)的构建
假设我们已经通过旧策略 π_old 采样了一条轨迹,并计算出了每个时刻的优势函数 A_t(具体公式见下文)。 那么,状态 s_t 的 目标价值 V_target(s_t) 通常定义为:
V_target(s_t) = A_t + V_θ_v(s_t)
_(注:这里 V_θ_v(s_t) 是采样时Critic的预测值)_
2. 损失函数(Value Loss)
Critic网络的更新目标是最小化预测值与目标值之间的均方误差(MSE)。 PPO通常会给Value Loss也加一个Clip操作(类似策略的Clip),以防止Value更新太猛破坏已经学到的特征。
不带Clip的简单形式:
L_value = (V_θ_v'(s_t) - V_target(s_t))^2
带Clip的形式(PPO标准做法):
V_clipped = V_θ_v(s_t) + clip(V_θ_v'(s_t) - V_θ_v(s_t), -ε, ε)
L_value = max( (V_θ_v'(s_t) - V_target(s_t))^2, (V_clipped - V_target(s_t))^2 )
通过梯度下降最小化这个 L_value,参数 θ_v' 就会被更新,使得下次预测的 V 更准。
第三部分:完整的 PPO (LLM Post-Training) 算法流程
下面是不省略符号的详细流程。
符号定义
- θ_π: Actor(策略网络/LLM)的参数。
- θ_v: Critic(价值网络)的参数。
- π_θ_π: 策略网络,给定Context
s 输出Token a 的概率。
- V_θ_v: 价值网络,估计状态
s 的价值。
- r(s, a): 奖励函数(通常由 RM 模型给出 + KL散度惩罚)。
- γ: 折扣因子(Discount Factor)。
- λ: GAE 平滑系数。
- ε: PPO Clip 阈值(如 0.2)。
- K: PPO 内部更新的 Epoch 次数。
- B: Batch Size。
算法流程
1. 初始化: 初始化 Actor 参数 θ_π 和 Critic 参数 θ_v。 初始化旧策略参数 θ_π_old。
2. 迭代循环(对于每一次 PPO Iteration):
步骤 2.1:采样 (Rollout) - 使用旧策略
- 从Prompt库中抽取一批 Prompts
{s_0^i}。
- 使用当前策略
π_θ_π_old 生成回复 {a_t^i},形成轨迹(Trajectory)。对于LLM,每个token生成都是一步。
- 计算每一步的奖励
r_t^i。在LLM中:r_t^i = r_RM(s_t^i, a_t^i) - β * log( π_θ_π_old(a_t^i|s_t^i) / π_θ_SFT(a_t^i|s_t^i) )
_(注:r_RM是奖励模型的打分,通常只在最后一步非零;β是KL惩罚系数;π_θ_SFT是SFT模型)_
- 关键: 使用当前冻结的 Critic
V_θ_v 计算所有状态的价值 V_θ_v(s_t^i)。
- 关键: 收集数据集
D = { (s_t^i, a_t^i, r_t^i, V_θ_v(s_t^i), π_θ_π_old(a_t^i|s_t^i) ) }。
步骤 2.2:计算广义优势估计 (GAE) - 数据预处理
- 对于每条轨迹,从最后一步向前递归计算 TD Error (
δ_t) 和 Advantage (A_t):
δ_t = r_t + γ * V_θ_v(s_{t+1}) - V_θ_v(s_t)
A_t = δ_t + γ * λ * A_{t+1}
_(如果是最后一步, V_θ_v(s_{T+1}) = 0)_
- 计算回报目标(Returns):
G_t = A_t + V_θ_v(s_t)。
- _至此,数据
D 扩充为包含 A_t 和 G_t 的固定训练集。_
步骤 2.3:PPO 内循环优化 (Epoch Loop) - 更新网络
- 令
π_old(a|s) = π_θ_π_old(a|s) (虽然公式里常用π_old指代采样时的策略,但在计算Ratio时,分母是采样时的概率,这部分是固定的)。
- 重复
K 个 Epochs (例如 K=4):
- 将数据集
D 打乱并划分为若干个 Mini-batch。
- 对于每个 Mini-batch
B:
- 计算新策略概率:计算当前
θ_π 下的 π_θ_π(a_t|s_t)。
- 计算概率比率 (Ratio):
r_t(θ_π) = π_θ_π(a_t|s_t) / π_old(a_t|s_t)
(注意:分母是步骤2.1里存下来的固定值)
- 计算策略损失 (Policy Loss):
L_policy = - min( r_t(θ_π) * A_t, clip(r_t(θ_π), 1-ε, 1+ε) * A_t )
(因为我们要最大化奖励,所以Loss取负号最小化)
- 计算价值损失 (Value Loss):
使用当前 Critic V_θ_v' 计算 V_θ_v'(s_t)。
L_value = (V_θ_v'(s_t) - G_t)^2
(这里使用了简单的MSE,也可以用带Clip的版本)
- 总损失 (Total Loss):
L_total = L_policy + c1 * L_value - c2 * S[π_θ_π](s_t)
(其中 S 是熵正则项,用于鼓励探索;c2 是系数)
- 反向传播与更新: 对
L_total 求导,使用 AdamW 优化器更新 θ_π 和 θ_v。
3. 更新旧策略:
- 完成
K 个 Epoch 后,本轮迭代结束。
θ_π_old <- θ_π (为下一轮 Rollout 做准备)。θ_v_old <- θ_v。
补充:Off-Policy中的重要性采样
重要性采样(Importance Sampling, IS)的根本原因,就是为了解决“用旧数据的分布,来估计新策略的期望”这一错位问题。 如果不引入这个机制,PPO 就无法在同一个 Batch 数据上进行多次更新(Epochs),数据利用率会极低。下面我通过 直观的例子、 数学原理 和 在 PPO 中的具体意义 三个层面为你详细拆解。
1. 直观理解:为什么需要“修正”?
场景假设:
- 旧策略(
π_old) :是一个喜欢“向左走”的人。他走了 100 次,有 90 次向左,10 次向右。
- 新策略(
π_θ) :参数更新后,变成了一个喜欢“向右走”的人。
现在,你想根据 旧策略走出来的这 100 次经验,来评估 新策略能得多少分。
- 问题:旧数据里大部分是“向左走”的经验。但新策略根本不爱向左走,这些经验对新策略来说重要吗? 不重要。
- 反之:旧数据里那稀缺的 10 次“向右走”的经验,虽然在旧策略看来是偶然,但对新策略来说却是 核心样本。
重要性采样的作用: 它相当于给每一个样本加了一个 权重(Weight) :
- 如果一个动作,新策略发生的概率比旧策略大(
π_θ/π_old > 1),说明这个样本对新策略很重要, 放大它的权重(Ratio > 1)。
- 如果一个动作,新策略发生的概率比旧策略小(
π_θ/π_old < 1),说明新策略很少会这么做, 缩小它的权重(Ratio < 1)。
2. 数学机理:变换概率分布的魔法
在强化学习中,我们的核心目标是最大化新策略 π_θ 的期望回报:
J(θ) = E_{a~π_θ(·|s)} [R(a)]
困境:我们手里没有 π_θ 产生的数据,只有 π_old 产生的数据。期望公式里的 a~π_θ 让我们没法直接算。我们在用“旧数据”评估“新策略”。PPO 的核心痛点是:数据是用旧策略 π_old 跑出来的,但我们想优化的是新策略 π_θ 的期望收益。
数学推导(Importance Sampling Trick): 我们可以乘一个“1”(即 π_old/π_old),把期望的下标换掉:
J(θ) = E_{a~π_θ} [R(a)] = E_{a~π_old} [ (π_θ(a|s) / π_old(a|s)) * R(a) ]
公式解析:
- 原本是在
π_θ 分布下求 R(a) 的平均值。
- 现在变成了在
π_old 分布下求 (π_θ/π_old) * R(a) 的平均值。
- 那个 Ratio
π_θ/π_old 就是“重要性权重”。
3. PPO 中的实战意义
比率 r_t(θ) 就是上面推导出的 Importance Weight。
为什么要这么做?(为了多轮更新)
- On-Policy 的局限(如 REINFORCE 算法):
- 采样一批数据 -> 算梯度 -> 更新一次参数
θ_π。
- 更新完
θ_π 变了,手里这批数据就“过期”了(失效了),必须扔掉重新采样。
- 效率极低。
- Off-Policy 的进化(如 PPO):
- 采样一批数据(此时存为
π_old)。
- Inner Loop (Epoch 1):用 IS 修正,更新
θ_π。此时 π_θ 和 π_old 差异很小,Ratio ≈ 1。
- Inner Loop (Epoch 2):
π_θ 变了一些,与 π_old 差异变大。此时 Ratio 开始偏离 1,IS 机制开始修正这种偏差,告诉梯度下降:“虽然这批数据是旧的,但我通过权重调整,假装它是新的。”
- Inner Loop (Epoch K):反复压榨这批数据的价值。
潜在风险与 PPO 的 Clip
重要性采样有一个致命弱点:如果 π_θ 和 π_old 差得太远,Ratio 会爆炸。
- 例如:旧策略概率 0.001,新策略概率 0.1。Ratio = 100。
- 这意味着这个样本的梯度会被放大 100 倍,导致更新步长过大,直接把策略训崩了。
这就是 PPO 引入 Clip 的原因:
L_policy = - min( r_t(θ_π) * A_t, clip(r_t(θ_π), 1-ε, 1+ε) * A_t )
PPO 说:“我允许你用旧数据来更新新策略,也就是允许 Ratio 偏离 1。但是! 别偏离太远(比如只能在 0.8 到 1.2 之间)。一旦超出这个范围,我就把你截断,不让你乱更新。”
4. 总结
- 根本原因:我们要最大化 新策略 的收益,但手里只有 旧策略 采的数据。
- 机理:通过乘上比率
π_θ/π_old,对旧数据进行加权。新策略越可能发生的样本,权重越大;越不可能的,权重越小。
- 价值:它打破了“采一次样只能更一次”的魔咒,让 PPO 可以在同一个 Batch 上跑多个 Epoch,极大地提升了数据效率(Sample Efficiency)。
总结图解
| 步骤 |
动作 |
使用的网络 |
输出/目的 |
| 1. Rollout |
这里的 θ_π 参与吗? |
Actor(θ_π_old), Critic(θ_v) |
产出 Trajectory (s,a,r) 和 V_θ_v(s) |
| 2. GAE计算 |
计算优势函数 |
仅仅是数学公式 |
产出固定标量 A_t 和 G_t |
| 3. Update |
计算 Loss |
Actor(θ_π), Critic(θ_v) |
Actor 使得 Ratio 增大 (在Clip范围内) Critic 使得 V_θ_v'(s) 逼近 G_t |
所以, 求状态价值函数 V 时使用了 GAE 这一说法是不准确的。准确的说法是: 更新 V 的参数时,使用了基于 GAE 计算出的 Return 作为标签。这就不存在套娃了。
再议PPO中方差与偏差的权衡(Bias-Variance Trade-off)
一、 为什么 returns = advantages + values 就是 λ-Return?
我们在代码里经常看到 returns = advantages + values,这个操作本质上是在 还原 回报。
根据优势函数(Advantage)的最原始定义:
A(s, a) = Q(s, a) - V(s)
或者在实际操作中,我们是用“真实回报”减去“基线(Baseline)”:
A(s, a) = R - V(s)
把公式移项,你会得到:
R = A(s, a) + V(s)
虽然 R 代表 Return,但它不是简单的 ∑γ^{t} r_t。 因为我们使用的是 GAE (Generalized Advantage Estimation),所以这个 R 是一个 混合了预测和现实的高级Return,学术上称为 λ-Return (G_t^λ)。但GAE 本质上就是一种计算 λ-Return 的技巧。我们可以证明:
G_t^λ = A_t^{GAE(γ, λ)} + V(s_t)
即:GAE优势 + 状态价值基线 = λ-回报。所以,Critic 更新的目标确实就是 λ-Return。我们将这个构建好的 G_t^λ 固定住(Detach / Stop Gradient),作为 Critic 回归任务(Regression)的 Label(标签)。
二、 深度解析 λ:偏差(Bias)与方差(Variance)的博弈
这里的 λ 是 GAE 中的衰减因子,它控制了我们 往未来看多远,或者说 多大程度上信任现实(Reward),多大程度上信任预测(Value)。公式回顾(TD Error)与 A_t^{GAE}:
δ_t^V = r_t + γ * V(s_{t+1}) - V(s_t)
A_t^{GAE(γ, λ)} = ∑_{l=0}^{∞} (γλ)^l δ_{t+l}^V
1. λ=0:One-step TD (纯预测)
当 λ=0 时,A_t^{GAE} = δ_t^V。 此时的目标回报 G_t^λ 变为:
G_t^{λ=0} = δ_t^V + V(s_t) = r_t + γ * V(s_{t+1})
- 含义:只看这一步的真实奖励
r_t,剩下的所有未来收益都完全信任 Critic 之前的预测 V(s_{t+1})。
- 偏差(Bias): 高。如果你的 Critic 网络一开始很烂(随机初始化),那么
V(s_{t+1}) 是错的,导致计算出的 G_t 也是错的。Critic 会朝着错误的目标更新。
- 方差(Variance): 低。因为只引入了一步的随机性(
r_t),数值比较稳定。
2. λ=1:Monte Carlo (纯现实)
当 λ=1 时,A_t^{GAE} = ∑_{l=0}^{∞} γ^l δ_{t+l}^V = ∑_{l=0}^{∞} γ^l r_{t+l} - V(s_t)。 此时的目标回报 G_t^λ 变为:
G_t^{λ=1} = ∑_{l=0}^{∞} γ^l r_{t+l}
- 含义:完全不信任 Critic 的预测,一直累加直到游戏结束(对于LLM是生成到
<eos>)。这就是真实的累计回报 Return。
- 偏差(Bias): 无(或低)。因为这是真实发生的奖励总和,是“真理”。
- 方差(Variance): 高。因为环境(或LLM采样)是随机的。同样的 Prompt,这次生成的回答拿了高分,下次生成的稍微不一样拿了低分。这种巨大的波动会导致 Critic 训练非常不稳定,难以收敛。
3. λ≈0.95:PPO 的黄金折中 (GAE)
PPO 选择 λ(通常在 0.9 到 0.99 之间),是为了 博采众长。
- 机制:它在计算回报时,是一个加权平均。既看重长远的真实奖励(Monte Carlo 的成分),又利用 Critic 的预测(TD 的成分)来平滑波动。
- 效果:
- 比
λ=1 方差小:因为引入了 Value Function 作为一个稳定的“锚点”,减少了随机采样带来的噪声。
- 比
λ=0 偏差小:因为更多地引入了多步的真实奖励,纠正了 Value Function 可能存在的估值错误。
三、 总结图表
参数 λ |
名称 |
计算公式 (简化) |
信任谁? |
偏差 (Bias) |
方差 (Variance) |
适用场景 |
| 0 |
TD(0) |
r_t + γ * V(s_{t+1}) |
信任 Critic(预测) |
高(网络不准就是误导) |
低(数据稳定) |
Value-based 方法 (DQN等) |
| 1 |
Monte Carlo |
∑γ^{t} r_t |
信任 Reality(现实) |
低(这是真实数据) |
高(噪声大,看运气) |
传统的 Policy Gradient (REINFORCE) |
| 0.95 |
GAE |
λ-Return |
混合(折中) |
中(平衡点) |
中(平衡点) |
PPO (SOTA 标准配置) |
结论
在 PPO 代码实现中,我们先算出 A_t,然后加上 V(s_t) 得到 G_t(即 λ-Return)。 这个 G_t 就是 Critic 苦苦追寻的“真理”(Label),Critic 的任务就是通过梯度下降,让自己输出的 V(s_t) 越来越接近这个 G_t。
GRPO算法
GRPO (Group Relative Policy Optimization) 是 DeepSeek 在其论文 DeepSeekMath 中提出的重要算法改进,它针对大语言模型(LLM)的特性,对传统 PPO 进行了极简主义的“手术”。
简单一句话概括:GRPO 是一种去除了 Critic 网络(价值函数),通过“组内归一化”来作为基线(Baseline)的 PPO 变体。
1. GRPO 在 PPO 上做了什么改进?
传统 PPO 的核心痛点是 显存占用大 和 训练复杂。
- PPO: 需要加载 Actor(策略模型)、Ref Model(参考模型)、Critic(价值模型)、Reward Model(奖励模型)。如果是全参数微调,显存压力巨大,通常 Critic 和 Actor 一样大。
- GRPO: 直接砍掉了 Critic(价值模型)。
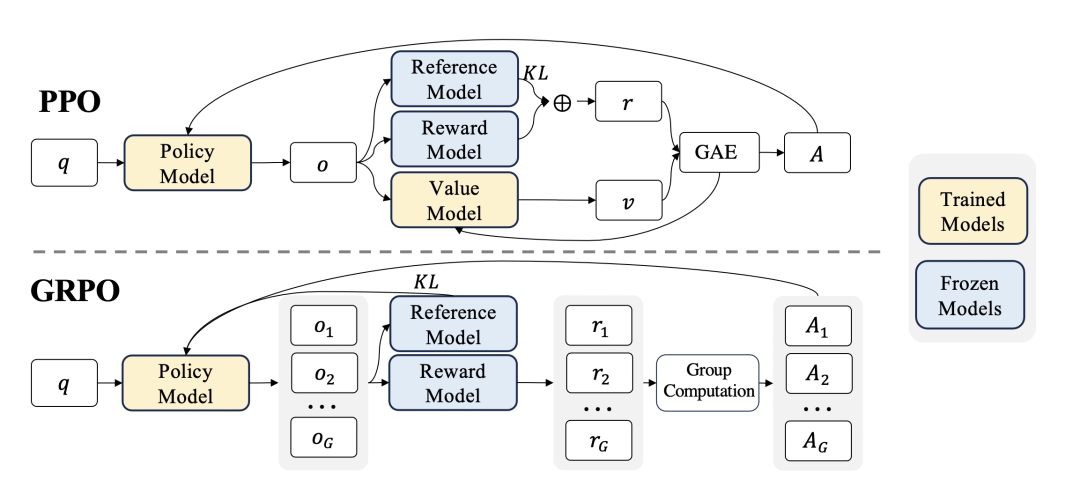
三大核心改进:
- 省略价值模型 (Critic-Free):不再需要一个神经网络来预测
V(s)。这直接节省了大量显存(约 50% 的模型参数内存),使得在同等硬件下可以训练更大的模型或使用更大的 Batch Size。
- 组内归一化基线 (Group-based Baseline):PPO 使用
V(s) 作为基线来减少方差(A = R - V(s))。GRPO 改为对于同一个 Prompt x,采样一组输出 {y_i},用这组输出的 平均奖励 作为基线。
- KL 散度外置 (KL Penalty in Loss):传统 PPO 通常将 KL 惩罚项加在 Reward 里(
r = r_rm - β*KL)。GRPO 在论文中倾向于直接在 Loss Function 中加入 KL 正则项,或者计算 Advantage 时处理,保持 Reward 的纯粹性(这取决于具体实现,但论文公式中 KL 是作为 Loss 的一部分出现的)。
2. 模型实现的细节:GRPO vs PPO
在强化学习的三个核心要素(State, Action, Reward)及优势计算上,GRPO 有显著变化:
| 要素 |
传统 PPO (LLM) |
GRPO (DeepSeekMath) |
核心区别 |
State (s) |
Prompt + 当前生成的 Token 序列 |
同左 |
无区别 |
Action (a) |
下一个 Token |
同左 |
无区别 |
Reward (r) |
由 Reward Model 给出,通常是标量。r_total = r_rm - β*KL |
由 Reward Model 或 规则检查器(如数学题判题) 给出。 |
GRPO 的 Reward 通常保持原始分数,不急着减 KL。 |
Value (V) |
神经网络预测。需要训练一个 Critic 网络 V_φ 拟合 V(s)。 |
无。不需要 Critic 网络。 |
最大不同点。 |
| Baseline |
V(s) (Critic 的输出) |
Group Mean(同组输出的平均分) |
用统计值代替预测值。 |
Advantage (A) |
A = r + γV(s') - V(s) (通常用 GAE) |
A_i = r_i - (1/N)∑_{j=1}^{N} r_j |
组内标准化。 |
3. 核心概念的精确定义 (RL Elements)
在 GRPO 中,我们要非常小心地区分“序列级(Sequence-level)”和“Token级(Token-level)”的变量。这是理解 GRPO 的关键。
- 状态 (State)
s_t: 不仅仅是 Prompt。对于第 t 步,状态是 Prompt x 加上之前已经生成的所有Token y_{<t}。
s_t = (x, y_{<t})
- 动作 (Action)
a_t: 当前步生成的 下一个 Token y_t。动作空间就是词表大小(Vocabulary Size)。
- 策略 (Policy)
π_θ: 就是我们的 LLM。输入状态 s_t,输出下一个 Token y_t 的概率分布。
- 奖励 (Reward)
R: 这是序列级别的。 环境(Reward Model 或 规则检查器)通常只在生成结束(EOS)时给出一个分数。 对于第 i 个采样结果 y_i,奖励为 R(y_i)。
注意:虽然奖励是序列级的,但它会通过 Advantage 广播到序列中的每一个 Token。
4. GRPO 的目标函数(Token-level Loss 详解)
这是 GRPO 的灵魂。让我们完全展开它,不省略任何求和符号。
L_GRPO(θ) = - (1/N) * (1/T) * ∑_{i=1}^{N} ∑_{t=1}^{T} [ min( r_t(θ) * A_i, clip(r_t(θ), 1-ε, 1+ε) * A_i ) ]
这里有几个极其重要的细节(推文重点):
- 双重求和 (
∑_{i=1}^{N} ∑_{t=1}^{T}):
- 外层
∑_{i=1}^{N}:对 Group 进行平均。即对同一个问题生成的 N 个回复进行遍历。
- 内层
∑_{t=1}^{T}:对 Token 进行平均。这就是强调的 Token 级别! 优化是针对每一个 token 的生成概率进行的。
- 优势函数
A_i 的广播机制:
A_i 是基于整句回复 y_i 的得分计算出来的(见下文)。- 但是!在计算 Loss 时,这个
A_i 被赋予给了这句话里的每一个 Token。
- 这意味着:如果这句话整体写得好(
A_i > 0),那么这句话里的每一个字(Token)都会被鼓励(概率增大);反之则每一个字都会被抑制。
- Token 级别的 KL 散度:
- 原文中 KL 是直接加在 Loss 里的,而且是 Per-Token 计算的。
- 公式为:
β * ∑_{t} [ π_θ(y_t|s_t) * (log π_θ(y_t|s_t) - log π_ref(y_t|s_t)) ](这是一种近似,或者使用标准的 KL(π_θ || π_ref))。
- 为什么要这样做? 相比于把 KL 减在 Reward 里(PPO的传统做法),把 KL 放在 Loss 里可以更直接地约束模型更新的步幅,防止模型针对某个 Token 的概率分布剧烈偏离 SFT 模型。
5. GRPO 完整训练流程
结合 DeepSeekMath 原文,这是一个严格的 Step-by-Step 流程:
Step 1: 生成 (Generation / Rollout)
- 给定一个 batch 的 Prompts
{x}。
- 对于每个
x,使用 旧策略 π_θ_old 进行 N 次独立采样,得到一组输出 {y_i}, i = 1,...,N。
- 这一步不进行反向传播,只保存 Log Probabilities 和 Token IDs。
Step 2: 评估与优势计算 (Evaluation & Advantage)
- 计算原始奖励:对每个完整的
y_i,计算奖励 R(y_i)。
- DeepSeekMath 场景:如果答案正确
R=1,错误 R=0。(也可以是特定格式分)。
- 计算组内优势 (Group Relative Advantage):
A_i = R(y_i) - (1/N) * ∑_{j=1}^{N} R(y_j)
A_i = (R(y_i) - μ) / (σ + ε) (实际常用标准化的版本)
- 关键点:
A_i 是一个标量,代表第 i 个回复在这一组里的“相对地位”。
Step 3: 构建 Token 级数据
- 将数据展开成 Token 级别。对于每一个 token
(i, t),它现在的“标签”包含两部分:
- 优势值:
A_i(来自它所属的整个句子)。
- 概率比率:
r_t(θ) = π_θ(y_{i,t} | s_{i,t}) / π_θ_old(y_{i,t} | s_{i,t})。
Step 4: 优化 (Optimization with PPO-Clip)
- 计算 Loss。
- PPO Clip:
L_policy = - min( r_t(θ) * A_i, clip(r_t(θ), 1-ε, 1+ε) * A_i )
- Add KL:
L_total = L_policy + β * KL(π_θ || π_ref)
(注意:最大化目标等于最小化负的 Loss)
- 反向传播更新参数
θ。
6. 优势函数的本质区别在哪里?
传统 PPO 的“Credit Assignment(信用分配)”是时间的。
- 它通过 GAE 试图分析:第 5 步的动作对第 10 步的奖励有多大贡献?
- 它依赖 Critic 网络来在时间维度上做差分 (
δ_t = r_t + γV(s_{t+1}) - V(s_t))。
GRPO 的“Credit Assignment”是空间的(组内的)。
- 它 放弃了时间维度的细粒度归因。它假设:如果这句话得了高分,那这句话里的 每个 Token 都是功臣。
- 它通过
A_i 告诉所有 token:“你们这组配合得好,大家一起加分”。
- 这也是为什么 GRPO 需要 KL 约束得更紧(Token-level KL):因为把整句的奖励分给每个 token 是一种很粗暴的近似(某些 token 其实是废话甚至是错的,但因为最终结果对而被奖励了),所以需要强力的 KL 正则来防止模型生成奇怪的 token。
总结:
GRPO 巧妙地将“价值预测问题”转化为了“组内排序问题”。它不再纠结于“这个 Token 到底值多少分”(这是 Critic 做的,很难做准),而是只问“这组回复里,哪一条比平均水平好?”。通过将序列级的相对优势 (A_i) 广播到 Token 级别的 PPO 损失函数中,DeepSeek 成功地去掉了 Critic,实现了在大模型推理任务上的高效 强化学习。
7. 为什么要这么做?创新点与目的解析
“为什么 DeepSeekMath 要用 GRPO 而不是 PPO”。
1). 针对“数学/推理”场景的特化
在数学推理任务中, 结果通常是二值的(对/错)。
- Critic 的困境:如果用传统 PPO,Critic 需要去拟合一个价值平面。但在数学题里,只要一步走错,价值可能瞬间从 1 掉到 0。这种稀疏且剧烈变化的 Reward 很难让 Critic 训练准确(High Variance)。
- GRPO 的优势:通过比较一组输出,直接看“谁比谁更好”。即使这道题很难,大家都错了(全 0 分),或者都很简单(全 1 分),标准差为 0(需要处理分母为0的情况,通常加个小量),或者归一化后能有效筛选出相对好的路径。它避开了“准确预测绝对分数”这个难题,只关心“相对排名”。
2). 极致的计算效率 (Efficiency)
- 显存解放:LLM 的 Critic 网络通常和 Actor 一样大(比如 7B 的 Actor 需要一个 7B 的 Critic)。砍掉 Critic,相当于节省了一半的显存!这意味着可以用更多的显存来存 Context,或者增大 Batch Size(这对 RL 稳定性至关重要)。
- 计算加速:少了一次 Critic 的前向传播和反向传播。
3). 利用 LLM 的多样性 (Diversity)
- LLM 生成本身具有随机性。GRPO 强制模型对同一个问题生成
N 次(比如 N=4)。这其实利用了 Self-Consistency (自洽性) 的思想。通过在 Loss 层面引入这种对比,模型能自然地学会“大概率导致正确结果”的模式,而不是偶然对一次的模式。
8. 其他重要的补充细节
- Iterative GRPO (迭代式 GRPO): 论文提到,随着训练进行,Ref Model 会定期更新(从旧的 Actor 变成新的 Ref)。但这在标准 GRPO 中不是必须的,通常 Ref Model 保持为 SFT 模型以防崩坏。
- Outcome Supervision vs Process Supervision: GRPO 非常适合 Outcome Supervision (结果监督)。因为只要最后答案对了,整条路径都被赋予正向 Advantage。这比训练一个能针对每一步打分的 Process Reward Model (PRM) 并在 PPO 中使用要便宜得多,也简单得多。
- KL 的处理细节: 在代码实现时,GRPO 的 KL 散度计算通常是 token-level 的。即:
KL_token = π_θ(y_t|s_t) * (log π_θ(y_t|s_t) - log π_ref(y_t|s_t))
这个项会加在 Loss 里,而不是像传统 PPO 那样去修改 Reward。这使得 A_i 的计算纯粹基于任务完成情况,使得优势估计更加“客观”。
总结
GRPO 并不是“套娃”或者是复杂的数学游戏,它是一次 奥卡姆剃刀 式的胜利。它敏锐地发现,在 LLM 这种生成式任务中,通过 自采样 (Self-Sampling) 构建的对比基线,比训练一个笨重且难以收敛的 Critic 网络要高效得多。对于 DeepSeekMath 这种需要大规模 强化学习 来提升推理能力的模型,GRPO 提供了低成本、高效率且稳定的解决方案。