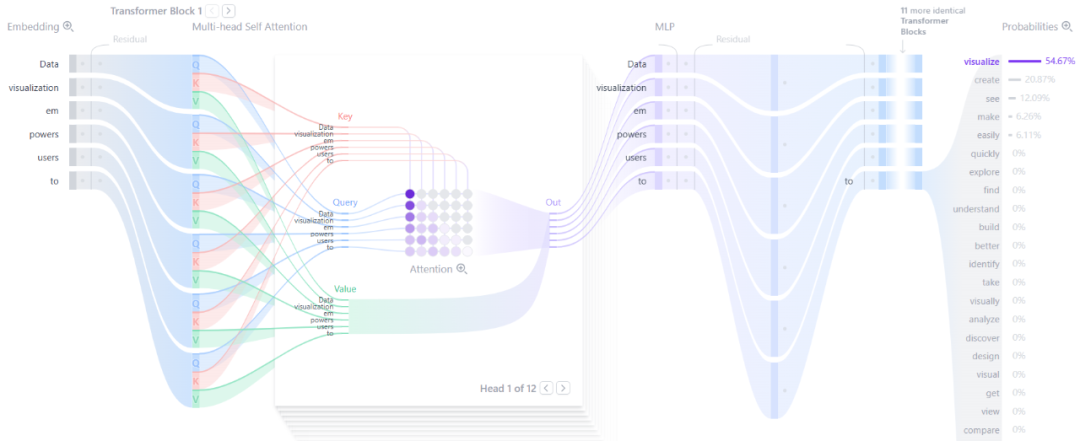
大模型(Large Language Model, LLM)技术的发展速度极快,半年前的前沿技术如今可能已成为基础知识。Polo Club 制作了一个 Transformer 模型的动态图解工具,对于直观理解 Transformer 的工作原理非常有帮助。此外,DeepSeek-V3 的论文内容极其丰富,从模型架构到基础设施都有详细阐述,并且已经开源,甚至包含了生产级的 MoE 实现细节。
引用
DeepSeek-V3 相关论文:
DeepSeek 开源资源:
总体架构
从上图可以看到,Transformer 模型本质上是由多个(几十个甚至上百个)Transformer Block 堆叠而成。当前主流的大模型基本都是 Decoder-only 架构,因为它更易于训练和优化性能,并能更好地利用 Scaling Laws 。早期研究就表明,增加神经网络的深度比增加宽度更有效,因为更深的网络类似于组合函数,具有更强的拟合能力,下层网络可以利用上层的中间结果。
下面详细解析图中的核心组件:
- Embedding 层:位于模型入口,它完成了分词(Tokenization)、词元嵌入(Token Embedding)和位置编码(Positional Encoding)三件事。分词基于词频识别词缀和词组,例如“un”、“ing”等。词元嵌入将 Token ID 映射为向量,这些参数与模型一同训练得到。位置编码(如正弦编码)则将词元在句子中的相对位置信息编码并融合进输入。
- Transformer Block:中间是堆叠的 Transformer Block,这种结构与几年前的卷积神经网络有相似之处。较低层的网络学习局部和语法模式,而较高层学习全局语义和推理,犹如一座“抽象之塔”。Attention 机制位于每个 Block 内部,下文将详解。
- 输出层:最后一个 Block 输出的向量会乘以一个大矩阵,上投影(up-project)到一个与词汇表大小相同的向量,称为 Logits。随后,选择 Logits 中值最大的 Top-K 个词元。最后,使用 Softmax 函数将 Logits 值转换为概率分布,并从中抽样输出一个词元。可选地,在进入 Softmax 前,可将 Logits 除以一个 Temperature 值。Temperature 越高,概率分布越平缓,模型输出的随机性也越高。
Embedding 技术在 Transformer 出现前已应用多年,它将词语转换为具有几何意义的高维向量。位置编码则与 Transformer 一同广为人知,其数学形式既简洁又精妙。输出层的 Softmax 是神经网络的常用方法。而 Transformer Block 中蕴含了大模型真正的核心——Attention 机制。
引用
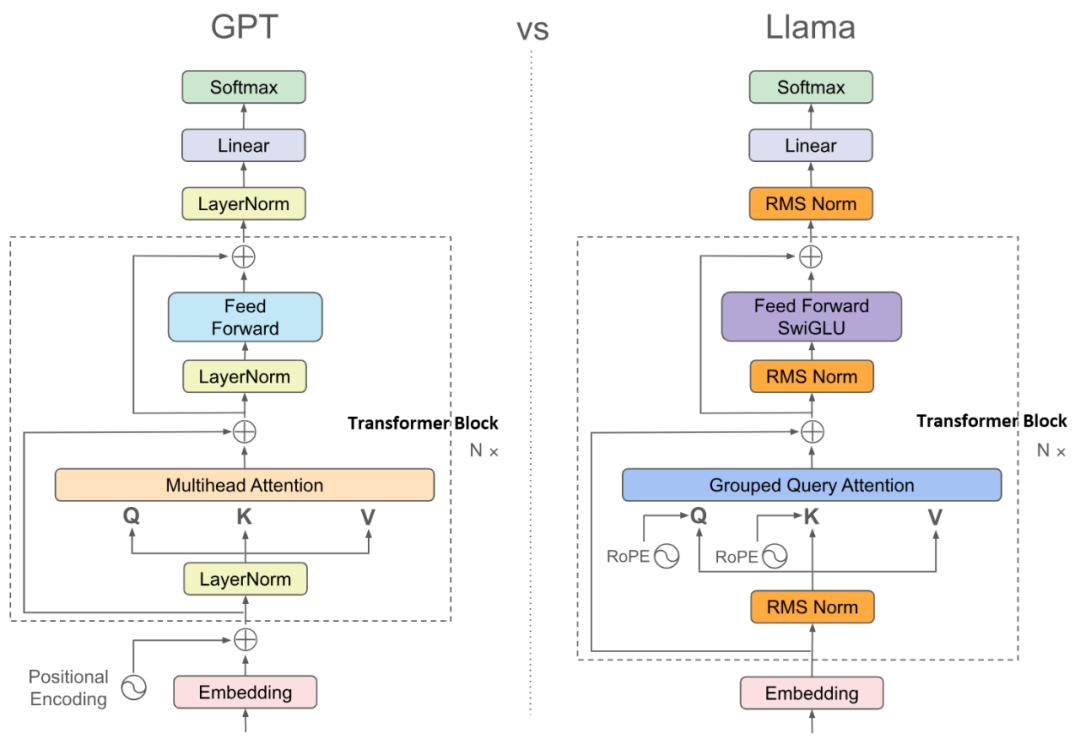
Transformer 模型的核心是 Transformer Block,它内部具体包含哪些组件呢?
- Attention 模块:这是 Transformer 魔力的来源,后续章节将详细阐述。其余部分则是经典的神经网络组件和一些优化技巧。
- 前馈神经网络(Feed-forward network, FFN):这本质上是一个基础神经网络。结构简单直接:输入层 -> 隐藏层 -> 输出层,隐藏层可以有多层。称为“前馈”是因为数据单向流动。它也常被称为多层感知机(MLP)或全连接网络(FCN)。
- RMSNorm(均方根标准化):神经网络层间常进行标准化以规范激活值的范围,防止梯度爆炸或消失。RMSNorm 因其参数更少、更易训练且能保留向量方向(不像 LayerNorm 会减去均值)而逐渐成为大模型的主流。
- 残差连接(Residual Connection):源自 ResNet。在深度网络中增加跨层连接,可以缓解深度带来的问题,如信息消失和错误累积,并帮助梯度在深层中有效传播。
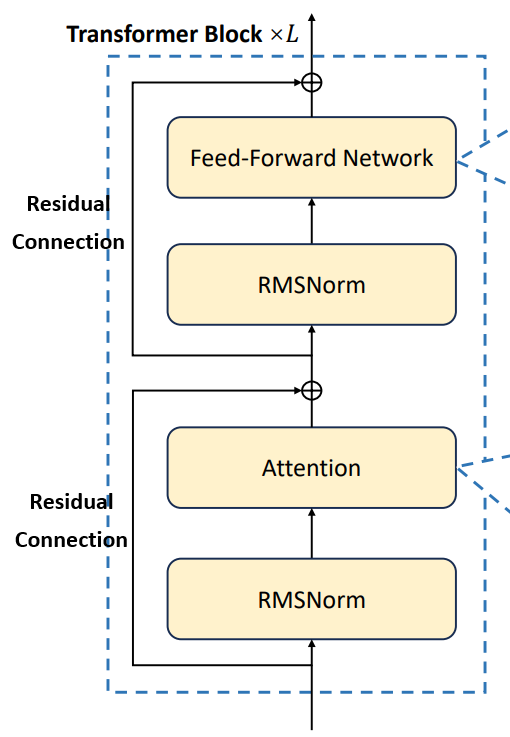
FFN 是神经网络的基础,已应用数十年。RMSNorm 也很常见,层间标准化是处理特征的标准方法。残差连接简单有效,自 ResNet 后便被广泛采用。而 Attention 才是真正的原创核心。
引用
Attention
Attention 是 Transformer 的关键。下图展示了其核心公式。
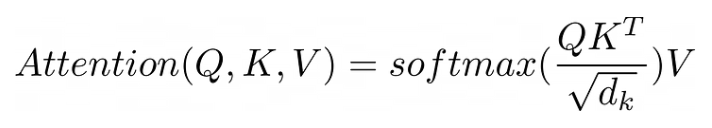
原公式信息密度很高,下面用更直白的伪代码展开,并逐项讲解:
// InputMatrix 的每一行是一个输入 Token 的 embedding 向量
// 行数是 Token 的总数
Q = InputMatrix * WeightMatrix_Q
K = InputMatrix * WeightMatrix_K
V = InputMatrix * WeightMatrix_V
// Attention 的公式
Attention = softmax((InputMatrix * WeightMatrix_Q
* WeightMatrix_K^T * InputMatrix^T)
/ sqrt(d_k))
* (InputMatrix * WeightMatrix_V)
逐项解析:
- 输入矩阵(InputMatrix):Transformer 以词元为输入,每个词元表示为向量。一次输入可能有数十至百万个词元,向量维度数百至数千。词元向量按行排列组成输入矩阵。
- *Q = InputMatrix WeightMatrix_Q**:Q 代表查询。在计算注意力前,输入先乘以权重矩阵得到 Q。K(键)和 V(值)同理。用权重处理输入是标准操作。
- QK^T:一个方形矩阵,维度等于词元总数。其元素是浮点值,由词元 i 和 j 的向量点积(经权重加权后)构成。形象地说,是文本序列中的词元在“相互注视”,这也是“自注意力”名称的由来。
- Sqrt(d_k):d_k 是词元向量的维度。假设 Q 和 K 的元素服从标准正态分布,QK^T 会将方差放大到 d_k。除以 sqrt(d_k) 这个缩放因子是为了将方差拉回 1。
- Softmax:按行作用于矩阵的标准归一化函数。经过 softmax,一行元素之和为 1,形似一组概率。QK^T 经此处理,变成了词元 i “关注”词元 j 的概率。
- *V:softmax(QK^T/sqrt(d_k)) 得到了自注意力概率。概率需要乘以“值”才能得到同量纲输出,V 就是加权的输入值。
总结而言,Attention 可视为给输入加上了两层权重:一层是作用于单个词元向量内部的 Q、K、V 权重(右乘),另一层是作用于词元之间的自注意力权重(左乘),后者使得不同词元的信息得以混合。
此外,Attention 还有两个要点:
- 多头(Multi-head):Transformer Block 中的 Attention 层是多头的,即同时运行多个独立的 Attention“头”,头数从十几到几十不等。这可能源于图像处理中多通道的思路。
- 掩码(Masking):在推理时,为了处理可变长度序列和实现因果预测(当前词元不能“看到”未来的词元),需要将后续或填充位置的注意力分数掩蔽为负无穷,以确保在 softmax 后概率为零。
引用
Attention 的几何形象
在理解基础公式后,可以从更直观的几何角度解释 Attention 的工作机制:
- Embedding:注意力计算的输入。它将词元转换为有几何含义的向量。向量夹角小、点积大,意味着对应词元语义相近。向量相加能混合语义。
- *Q = InputMatrix WeightMatrix_Q**:词元向量并非直接参与计算,而是先乘以 Q 权重矩阵。可以将权重矩阵的列视为另一组“尺子”,相乘是在测量词元与这些尺子的相似度,输出 Q 则是以这些尺子为基准重建的词元表示。K 同理。
- 位置编码:以 RoPE 为例,它实质上是将词元向量旋转一个角度。位置越靠后,旋转角度越大。这样,相邻词元的向量夹角更小,点积(注意力分数)更高。
- QK^T:计算所有词元对之间的点积作为注意力分数。因此,两个词元语义越近、在句子中位置越近,它们的注意力分数就越高。
- *V:最后将注意力分数与 V 矩阵相乘,本质上是根据分数权重混合各个词元的向量。注意力机制的输出,是原始词元向量与其所“关注”的上下文信息的混合体。
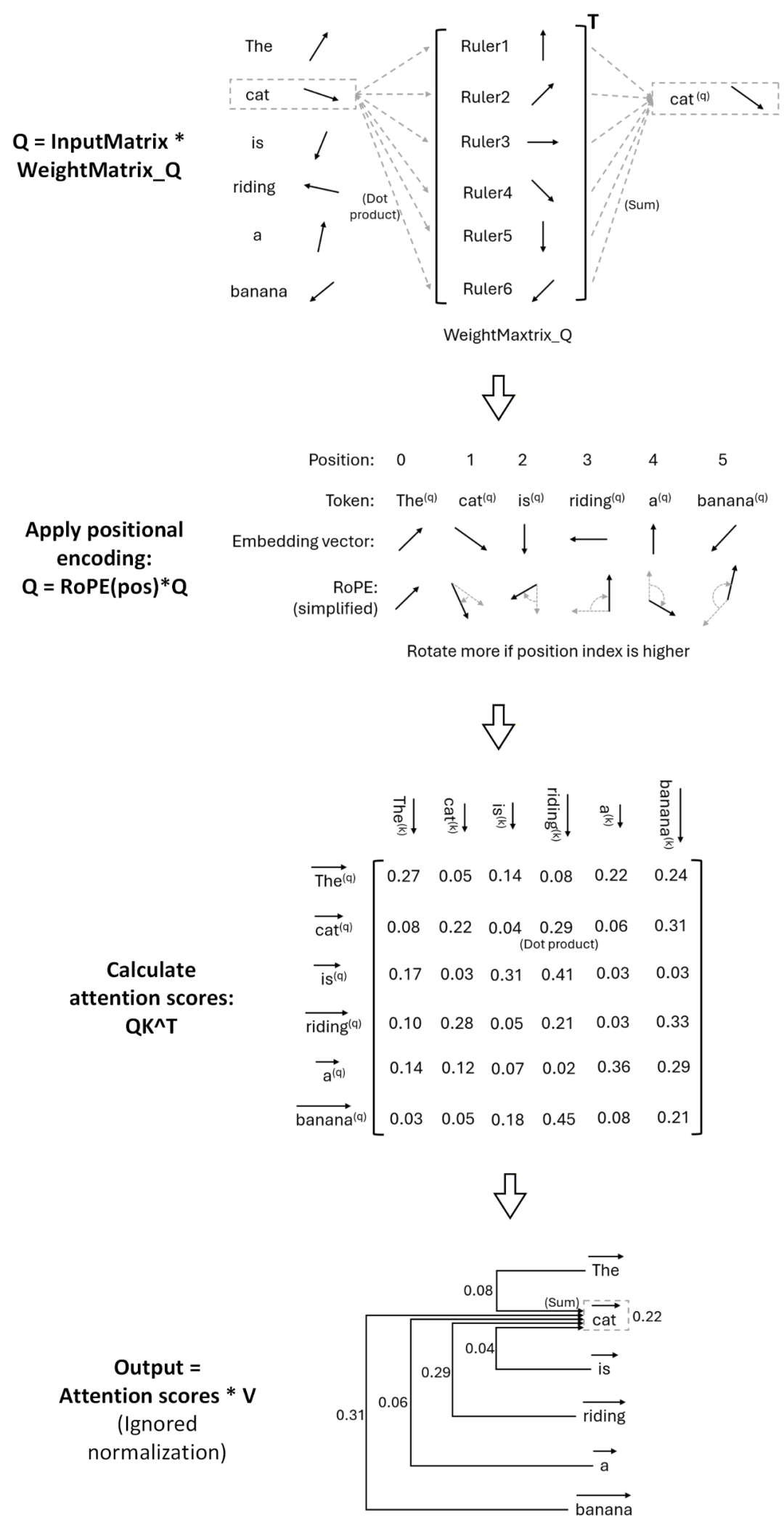
这个几何视角揭示了一个关键点:注意力分数本质是计算词元向量间的相似性。如果没有位置编码,注意力将对词元的顺序无关(排列不变性)。因此,引入位置编码是必须的。
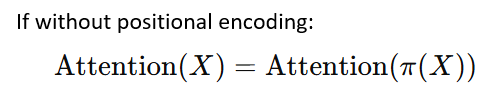
KV Cache
注意力机制的另一大优势在于其可增量计算的特性。理论上,处理长度为 N 的序列需要计算 N×N 的注意力矩阵。但实际上,推理时可以逐个词元递进计算,复用之前的结果,这就是 KV Cache 的思想。
下图和对应的动态图清晰地展示了 KV Cache 的计算过程:
- 计算词元 2 时,需要 Value 1~2,Key 1~2 和 Query 2。
- 计算词元 3 时,需要 Value 1~3,Key 1~3 和 Query 3。其中 Value 1~2 和 Key 1~2 可复用上一步的结果。
- 计算词元 4 时,依此类推。
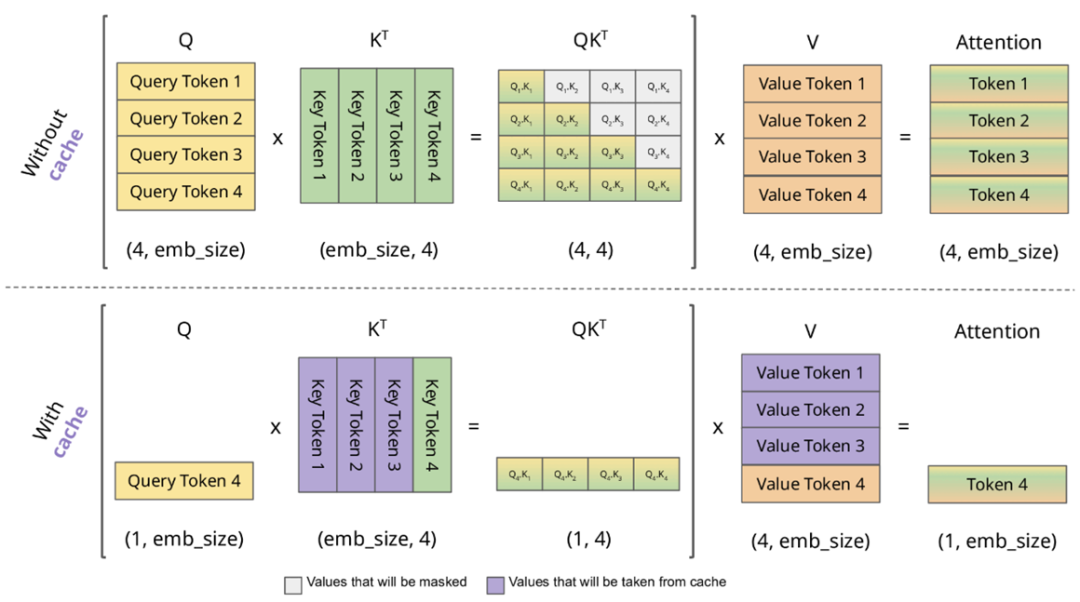
计算下一个词元时,总是需要之前所有词元的 Key 和 Value,它们可以被递进地复用,因此适合缓存。而 Query 只需当前词元,故无需缓存。这也解释了为什么用户上下文越长,KV Cache 占用的内存就越大,成本越高。
需要注意的是,KV Cache 依赖于之前计算过的确切词元。如果上下文中间的词元发生变化,后面的 Cache 便无法复用。因此,KV Cache 常作为 前缀缓存(Prefix Cache) 实现。这也解释了为什么在 Agent 设计中,不变的 系统提示(System Prompt) 放在开头,其 KV Cache 可以跨对话复用。
由于 KV Cache 的存在,Transformer 推理常分为两个阶段:
- Prefill 阶段:处理用户输入的整个提示文本,生成并缓存所有 Key 和 Value。此阶段计算并行度高,瓶颈常在 GPU 算力。
- Decode 阶段:基于 KV Cache 逐个词元地生成输出。此阶段计算是串行的,瓶颈常在于内存(显存)带宽和容量。
引用
Multi-Head Latent Attention (MLA)
接下来介绍 DeepSeek-V3 论文中的 Multi-Head Latent Attention (MLA)。它的核心“魔法”是通过降维投影压缩来减少 KV Cache 的占用,从而提升推理效率,且测试表明这种压缩对模型性能影响很小。
在下图公式中:
- 蓝框中的向量是需要被缓存的。
h_t 表示词元向量,是注意力计算的输入。W^D* 表示降维投影矩阵,W^U* 表示升维投影矩阵。k, q, v 分别指 K, Q, V 向量。k_t,i 中,t 表示第 t 个词元,i 表示第 i 个头。c* 是 MLA 引入的潜在向量,即经过压缩的中间表示。*R 表示应用了 RoPE 位置编码。
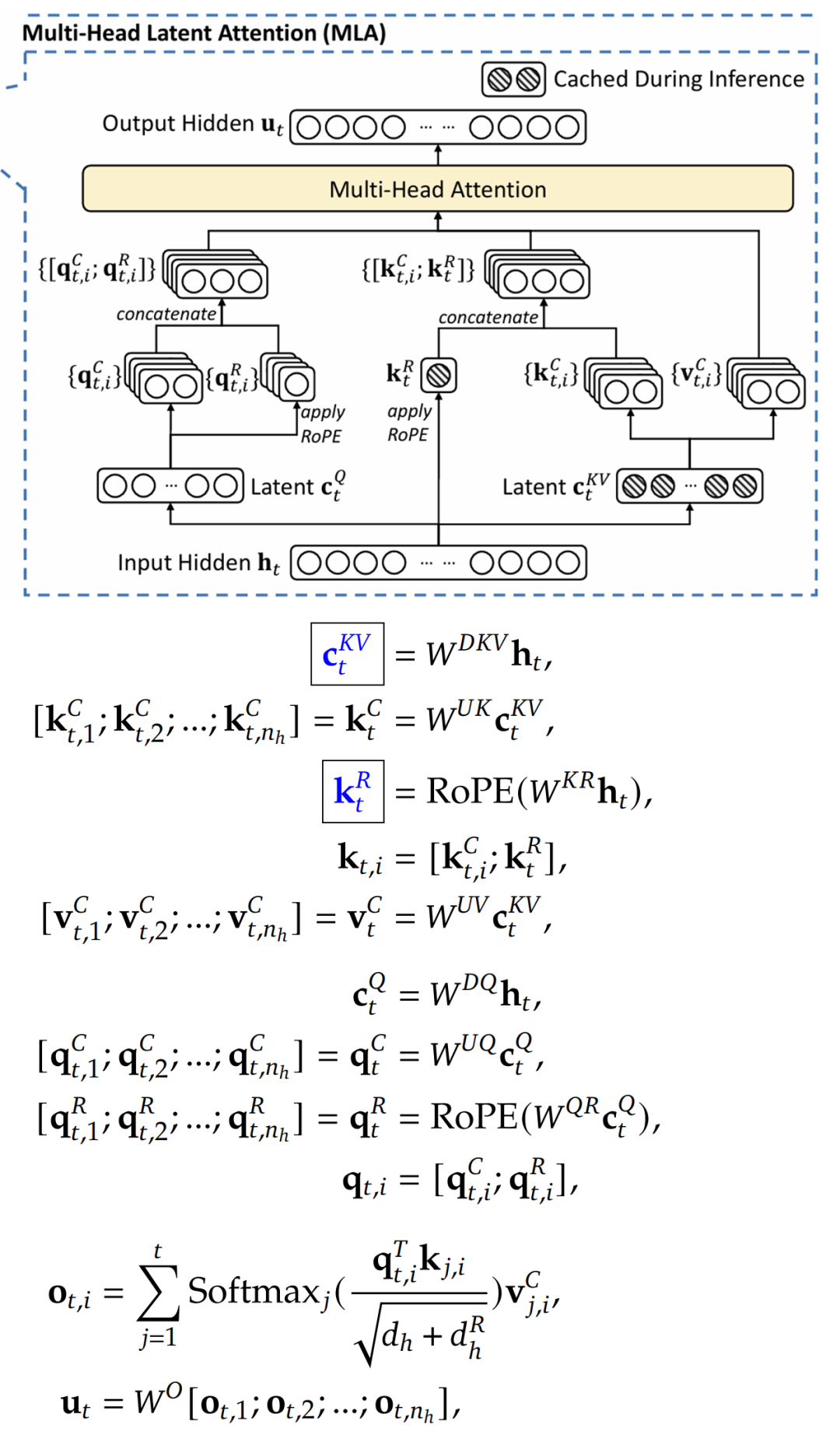
MLA 组件解析:
- 图中右半边(K, V 路径):不同于普通注意力直接用
h_t 计算 K 和 V,MLA 先将 h_t 降维投影到 c_t^KV。缓存的是 c_t^KV,而不是为每个头分别缓存 K 和 V,这大大减少了缓存占用。然后,c_t^KV 再被升维投影还原出计算所需的 K 和 V。
- 图中左半边(Q 路径):Q 的处理类似,也先降维到
c_t^Q,再升维还原。Q 不需要被缓存。
- 带有 R 的部分:MLA 为 K 和 Q 的向量额外增加了 RoPE 位置编码路径(
k_t^R, q_t,i^R)。最终输入注意力计算的向量由升维投影得到的向量和 RoPE 编码后的向量拼接而成。k_t^R 在所有注意力头间共享,进一步节省缓存。
- 最终计算:处理后的 K, Q, V 输入标准的 多头注意力 进行计算。
由此可见,节省 KV Cache 的关键在于降维投影压缩。RoPE 位置编码则被解耦到独立路径处理。这种降维投影技巧在 人工智能 领域也被称为 低秩压缩,与存储压缩不同。例如:
- LoRA:微调时,参数更新 ∆W 可分解为两个小矩阵 B*A 的乘积,极大减少了微调参数量。
- MLP 扩展/压缩:在 FFN 层中,常将输入维度先升维(如 768 -> 3072)计算后再降维回去,高维空间为知识存储和非线性表达提供了容量。
引用
关于 MLA 更深入的问题
理解了 MLA 原理后,可以进一步探讨几个深入问题:
为什么 RoPE 要与 K、Q 的降维投影分开计算?
可以理解为,在 Attention 公式 QK^T = ... 中,权重矩阵 WeightMatrix_Q * WeightMatrix_K^T 可以融合为一个固定矩阵 M 来简化计算。但如果中间插入了对位置敏感的 RoPE,M 就不再固定,无法提前融合。论文解释为:RoPE 与低秩 KV 不兼容,因为 RoPE 使 Q 和 K 都与位置相关,若将 RoPE 应用于 k_t^C,会导致权重矩阵 W^UK 与位置矩阵耦合,从而无法被吸收简化。
Q 不需要缓存,为什么也需要降维投影到 c_t^Q?
这是经典的低秩压缩技巧。假设 h_t 维度为 7168,目标 Q 维度为 1536。直接使用一个大矩阵 W (71681536) 降维参数量大。而分解为 W^DQ (7168512) 和 W^UQ (512*1536) 两个矩阵,参数总量更少。论文指出这有助于减少训练中的激活内存占用。
为什么每个 Attention 层都要做 RoPE,而不是只在开头做一次?
老式 Transformer 使用的绝对位置编码是在开头加一次,通过残差连接传递。而 RoPE 的设计就是在每个注意力计算前对 Q 和 K 应用旋转。另一方面,由于 RoPE 与降维投影不兼容,也需要在每个注意力层前重新应用,并与降维路径解耦。
应该先应用 RoPE 还是先乘以权重矩阵得到 Q/K?
与绝对位置编码在乘权重矩阵之前添加不同,RoPE 要求应用在乘以权重矩阵之后。这是因为 RoPE 是乘法旋转操作,如果应用在权重矩阵之前,旋转带来的几何角度信息会被后续的线性变换破坏。
为什么 V 不需要应用 RoPE 位置编码?
使用 RoPE 是为了让 Q 和 K 能根据位置信息计算注意力分数。V 保存的是词元的原始信息,用于与注意力分数加权求和,没有必要再进行旋转。
RoPE 的旋转有周期性,会导致远距离词元“撞周期”吗?
RoPE 并非简单旋转整个向量。它将向量分成多个 2D 分量,每个分量以不同速度旋转(低维快,高维慢)。虽然单个分量有周期性,但所有分量组合起来,整个向量很难发生周期碰撞。这种设计使得低维分量更关注局部信息,高维分量更关注全局语义。
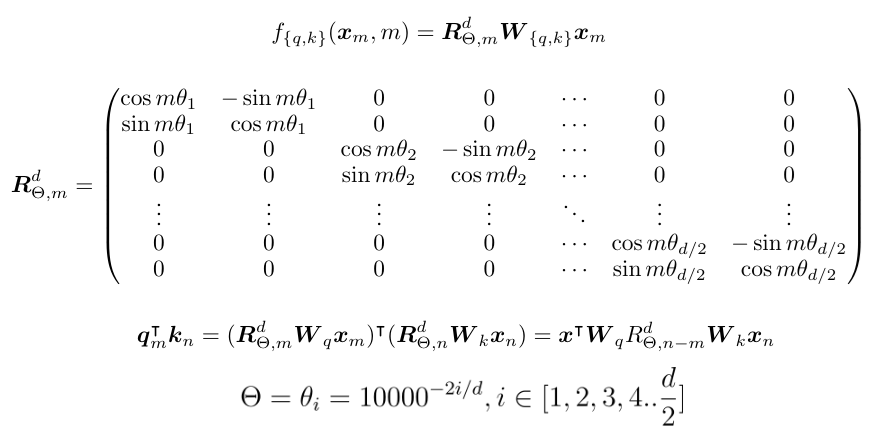
引用
Mixture of Experts (MoE)
DeepSeek 论文还详细讲解了生产级的 Mixture-of-Experts 实现。MoE 已成为新一代大模型的标配,它能支持巨大参数量下的稀疏激活。在 MoE 中,Transformer Block 的 FFN 层被替换为 MoE 层:
- 不同于单个稠密 FFN,MoE 将其拆分为许多更小的 FFN 模块,称为“专家”。专家可以并行计算。
- 对于每个输入词元,只激活部分专家,实现了“稀疏”性,大幅降低了训练和推理的计算成本。
- 一些专家总是被激活,称为共享专家。
- MoE 引入了路由机制,它是 MoE 的关键,需要保证负载均衡,并为词元选择最合适的专家。
DeepSeek-V3 每层 MoE 有 256 个专家,每个词元会激活其中 Top-8 个专家以及共享专家,结果被合并输出。
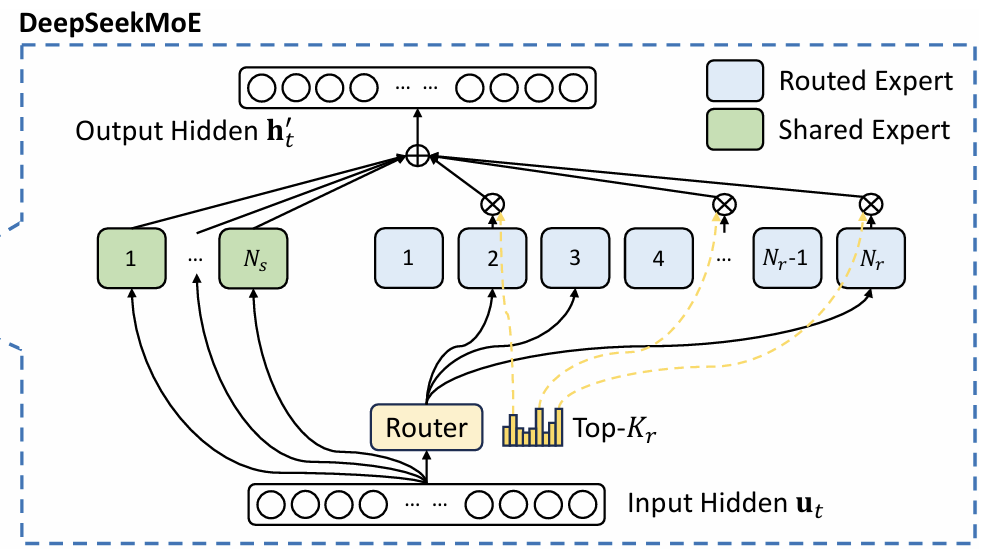
MoE 路由机制:
下图公式展示了路由过程:
u_t 是输入词元,h_t' 是 MoE 输出。- 每个专家有一个可训练的质心向量
e_i。计算输入与所有质心的相似度,取相似度最高的 Top-K 个专家激活,门控值记为 g_i,t。
- 实际路由门控还需包含负载均衡修正和惩罚项(见论文公式)。
- 路由本身可以看作一个小的神经网络,专家质心是其可训练的参数。
- 在输出公式中,激活专家的输出、共享专家的输出以及输入本身(残差连接)直接相加得到最终结果。
MoE 的挑战在于确保专家负载均衡,避免“专家崩溃”(少数专家处理多数词元)或“专家饥饿”(某些专家训练不足)。MoE 能减少激活参数量和计算量,利于专家并行,但并不会减少模型加载所需的内存,因为所有专家参数都需载入。
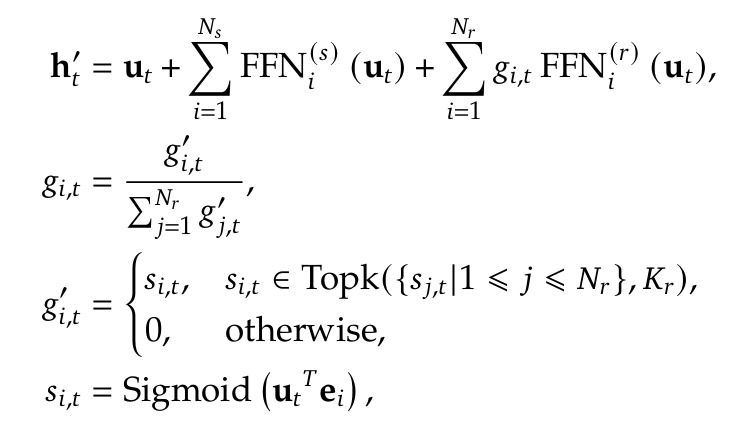
为什么对 FFN 层使用 MoE,而不是 Attention 层?
一方面,FFN 独立处理每个词元,更易于切分和并行;而 Attention 处理的是词元对之间的关系。另一方面,FFN 层通常占据了 Transformer 的大部分参数,远多于 Attention 层。
引用
总结
本文系统性地介绍了 Transformer 的基础知识,涵盖模型架构、核心组件、Attention 机制及其优化 KV Cache,并深入探讨了 MLA 和 MoE 等高级主题。DeepSeek 的论文为理解大模型从理论到工程的方方面面提供了宝贵资料。同时,Polo Club 的动态可视化工具让 Transformer 的学习过程变得更加直观和互动。对于希望深入 开源实战 领域的开发者而言,研究这些顶尖的 开源项目 是极佳的学习路径。更多前沿技术讨论与资源分享,欢迎访问 云栈社区。